بالنسبة لمعظم الناس ، تعتبر الكسور أول العمليات الحسابية المعقدة التي يتم العثور عليها. مفهوم الكسور صعب للغاية ويتطلب منك تعلم شروط خاصة للقيام بذلك. نظرًا لأن الكسور لها قواعد خاصة للجمع والطرح والضرب والقسمة ، فإن الكثير من الناس مرتبكون حيال ذلك. ومع ذلك ، مع الكثير من الممارسة ، يمكن لأي شخص أن يتعلم ويكمل العمليات الحسابية المتعلقة بالكسور.
خطوة
طريقة 1 من 5: فهم الكسور
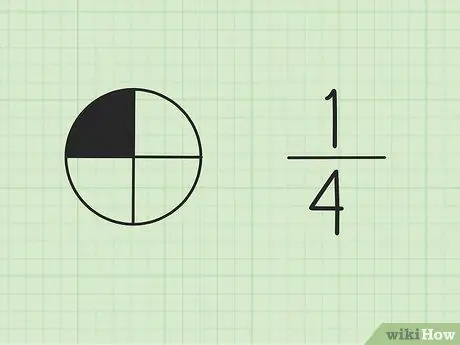
الخطوة الأولى: افهم أن الكسور جزء من الكل
الرقم الموجود في الأعلى يسمى البسط ، ويمثل عدد أجزاء الإجمالي. الرقم الموجود في الأسفل يسمى المقام ، والذي يمثل العدد الإجمالي للأجزاء.
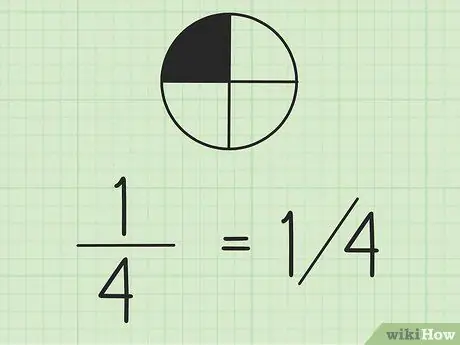
الخطوة 2. ضع في اعتبارك أنه يمكنك كتابة الكسور باستخدام الشرطة المائلة
الرقم الموجود على اليسار هو البسط والرقم الموجود على اليمين هو المقام. إذا كنت تعمل مع كسور على نفس السطر ، فمن الأفضل أن تكتب البسط فوق المقام.
على سبيل المثال ، إذا أخذت واحدة من أربع شرائح بيتزا ، فلديك بيتزا. إذا كان لديك 7/3 بيتزا ، فهذا يعني أن لديك 2 بيتزا كاملة بالإضافة إلى شريحة من 3 شرائح بيتزا
الطريقة 2 من 5: الفرق بين الكسور المختلطة والبسيطة
الخطوة الأولى: افهم أن الأعداد المختلطة تتكون من أعداد صحيحة وكسور ، على سبيل المثال 2 1/3 أو 45 1/2
عادة ، يجب عليك تحويل الأرقام المختلطة إلى صيغة أبسط للجمع أو الطرح أو الضرب أو القسمة.
الخطوة الثانية. غيّر الرقم المختلط بضرب الرقم الصحيح في المقام في الكسر ، ثم جمعه في البسط
اكتب النتيجة على أنها البسط ، بينما المقام لا يتغير.
على سبيل المثال ، لتحويل 2 1/3 إلى كسر بسيط ، اضرب 2 في 3 ، ثم أضف 1 واحصل على 7/3
الخطوة الثالثة. تحويل الكسور البسيطة إلى أعداد كسرية بقسمة البسط على المقام
تتم كتابة النتيجة الكاملة للقسمة في صورة عدد صحيح ، ويتم كتابة باقي القسمة على هيئة بسط الكسر. المقام لا يتغير.
على سبيل المثال ، لتحويل 7/3 إلى رقم كسري ، قسّم 7 على 3 لتحصل على 2 مع باقي 1. وبالتالي فإن الرقم المختلط هو 2 1/3. لا يمكن تحويل الكسور البسيطة إلى أعداد كسرية إلا إذا كان البسط أكبر من المقام
طريقة 3 من 5: جمع وطرح الكسور
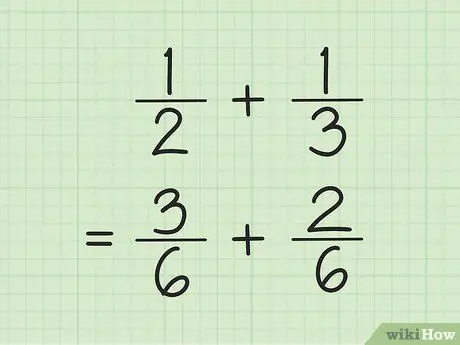
الخطوة 1. أوجد مقامًا مشتركًا لجمع الكسور وطرحها
الحيلة ، اضرب الأرقام في المقام ، ثم اضرب كل بسط في الرقم المستخدم لإيجاد المقام. في بعض الأحيان ، يمكنك إيجاد المضاعف المشترك الأصغر (المضاعف المشترك الأصغر) للمقام بضرب المقام في الآخر.
على سبيل المثال ، لجمع و 1/3 ، أوجد أولاً المضاعف المشترك الأصغر (المضاعف المشترك الأصغر) للمقامرين بضرب بعضهما البعض. وهكذا ، تضرب 2 و 3 لتحصل على المضاعف المشترك الأصغر 6. اضرب 1 في 3 لتحصل على 3 كبسط جديد للكسر الأول. اضرب 1 في 2 لتحصل على 2 كبسط جديد للكسر الثاني. الكسور الجديدة هي 3/6 و 2/6
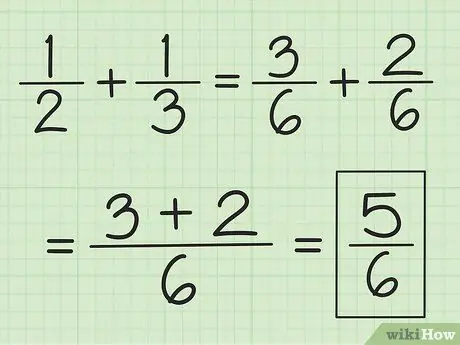
الخطوة الثانية: اجمع البسطين معًا ولا تغير المقام
على سبيل المثال ، 3/6 زائد 2/6 يساوي 5/6 ، و 2/6 زائد 1/6 يساوي 3/6
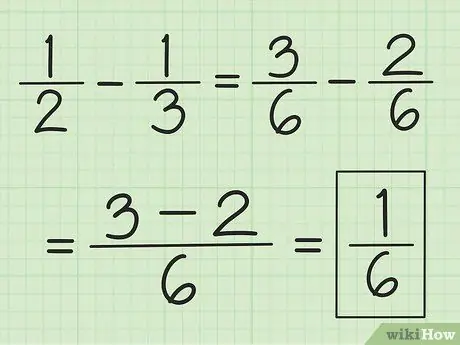
الخطوة 3. استخدم أسلوبًا مشابهًا للطرح
أوجد المضاعف المشترك الأصغر للمقام أولًا ، لكن بدلًا من جمعهما ، اطرح رقم البسط الأول من رقم الثاني.
على سبيل المثال ، لطرح 1/3 من 1/2 ، قم أولاً بتغيير الكسور إلى 3/6 و 2/6 ، ثم اطرح 3 في 2 للحصول على 1. ينتج عن هذا 1/6
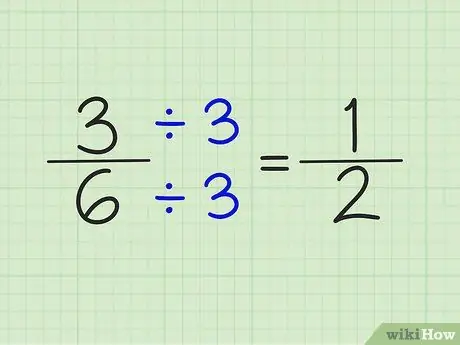
الخطوة 4. بسّط الكسور بقسمة البسط والمقام على نفس العدد
على سبيل المثال ، الرقم 5/6 لا يمكن تبسيطه. ومع ذلك ، يمكن تبسيط 3/6 بقسمة البسط والمقام على الرقم 3. والنتيجة هي كسر 1/2
الخطوة 5. حوّل الكسر إلى عدد كسري إذا كان البسط أكبر من المقام
طريقة 4 من 5: اضرب وقسم الكسور
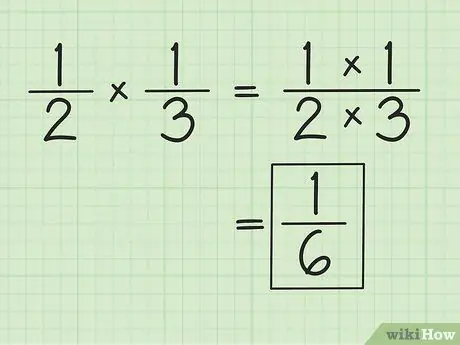
الخطوة 1. اضرب البسط والمقام بشكل منفصل لضرب الكسور
على سبيل المثال ، عند الضرب في 1/3 ، تكون النتيجة 1/6 (1 مرات 1 ، و 2 مرات 3). لست بحاجة إلى مطابقة المقامات عند ضرب الكسور. تبسيط أو تعديل النتائج التي تم الحصول عليها ، إذا لزم الأمر
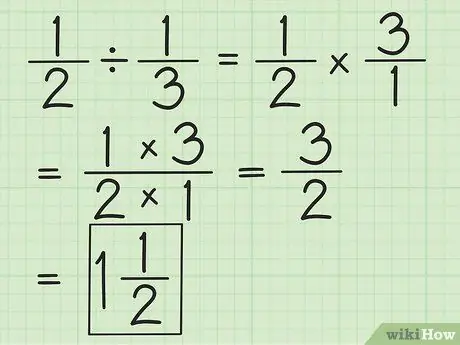
الخطوة الثانية. قسّم كسرين بقلب الكسر الثاني ، ثم ضرب كليهما
على سبيل المثال ، إذا كنت تريد قسمة 1/2 على 1/3 ، فعليك أولاً عكس الكسر الثاني إلى 3/1. اضرب في 3/1 واحصل على 3/2. بسّط الكسور أو حوّل إلى أعداد كسرية إن أمكن
طريقة 5 من 5: التعامل مع الكسور المركبة
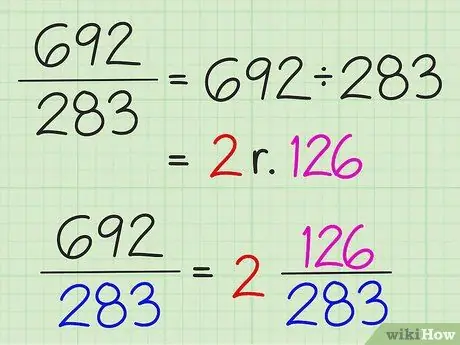
الخطوة 1. حلل كل الكسور بنفس الطريقة ، حتى لو بدت المشكلة معقدة للغاية
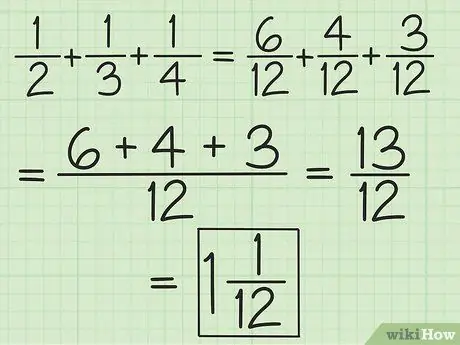
الخطوة 2. قم بمطابقة المقامات لجميع الكسور أو اعمل في أزواج بدءًا من اليسار إلى اليمين لجمع وطرح أكثر من كسرين
على سبيل المثال ، لإضافة 1/2 و 1/3 و 1/4 ، يمكنك تغييرها إلى 6/12 و 4/12 و 3/12 للحصول على 13/12 ، أو يمكنك إضافة 3/6 و 2 / 6 تحصل على 5/6 ثم أضف 5/6 و 1/4 (معادلة المقامات بحيث يصبح الكسر الثاني 3/12) لتحصل على 13/12 (10/12 زائد 3/12). حوله إلى عدد كسري ، وهو 1 1/12
نصائح
- تذكر أنك تعلمت الكثير من الرياضيات. الرياضيات مثل اللغة التي يمكنك نطقها بطلاقة ، وأنت الآن تحاول تعلم القراءة والكتابة.
- تذكر دائمًا تبسيط النتيجة النهائية لعملية الحساب ، سواء كانت مشكلتك في صورة كسر عادي أو عدد كسري أو كسر مركب.
