- مؤلف Jason Gerald [email protected].
- Public 2024-01-15 08:08.
- آخر تعديل 2025-01-23 12:06.
الطرح هو ببساطة طرح رقم واحد من رقم آخر. من السهل طرح عدد صحيح من آخر ، ولكن قد يكون الطرح صعبًا إذا كنت تطرح كسوراً أو كسوراً عشرية. بمجرد فهمك للطرح ، ستتمكن من استخدام مفاهيم رياضية أكثر تعقيدًا ، وستكون قادرًا على جمع الأرقام وضربها وقسمتها بسهولة أكبر.
خطوة
الطريقة 1 من 6: طرح أعداد صحيحة كبيرة بالاقتراض

الخطوة 1. اكتب عددًا كبيرًا
على سبيل المثال ، تريد حل 32 - 17. اكتب 32 أولاً.

الخطوة 2. اكتب الرقم الأصغر أسفله مباشرةً
تأكد من وضع قيم العشرات والآحاد في الأعمدة الصحيحة ، بحيث تكون 3 من 32 أعلى مباشرة من 1 من 17 و 2 من 32 أعلى مباشرة من 7 من 17.
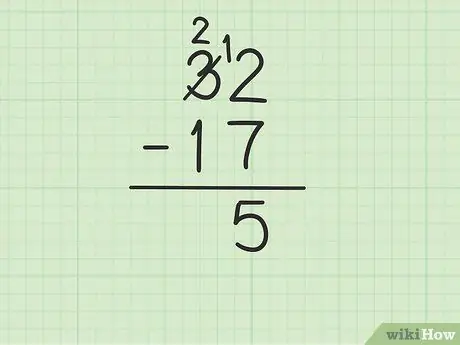
الخطوة 3. اطرح الرقم العلوي في عمود الوحدات من الرقم الموجود في الأسفل
ومع ذلك ، يمكن أن يصبح هذا معقدًا إذا كان الرقم السفلي أكبر من الرقم العلوي. في هذه الحالة ، 7 أكبر من 2. إليك ما عليك القيام به:
- عليك الاقتراض من الرقم 3 من 32 (المعروف أيضًا باسم التجميع) لتحويل 2 إلى 12.
- اشطب الرقم 3 من 32 واستبدله بالرقم 2 ، بينما يصبح الرقم 2 12.
- يمكنك الآن طرح 12-7 ، وهو ما يساوي 5. اكتب 5 تحت العددين اللذين تطرحهما حتى يكونا في عمود الوحدات في الصف الجديد.
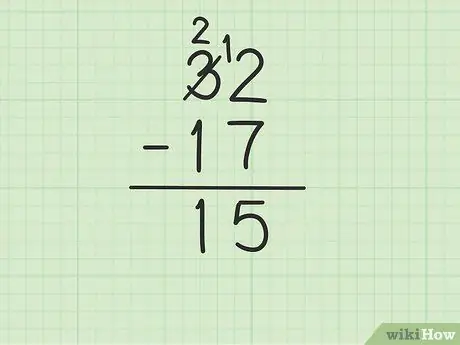
الخطوة 4. اطرح الرقم العلوي في عمود العشرات من الرقم السفلي
تذكر 3 أصبح 2. الآن اطرح 1 من 17 من 2 أعلاه لتحصل على (2-1) 1. اكتب 1 أدناه ، في عمود العشرات ، على يسار 5 في عمود الوحدات. تكتب 15. أي 32 - 17 = 15.
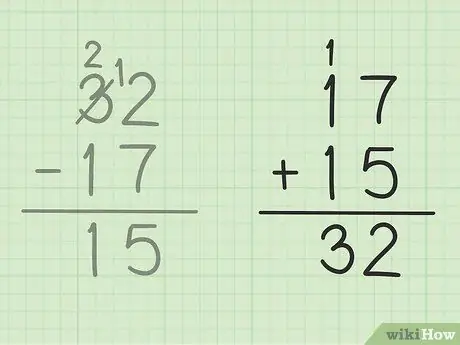
الخطوة 5. تحقق من عملك
إذا كنت تريد التأكد من طرح رقمين بشكل صحيح ، فكل ما عليك فعله هو جمع إجابتك مع الرقم الأصغر لتكوين رقم كبير. في هذه المسألة ، يجب أن تضيف إجابتك ، 15 إلى عدد الطرح الأصغر ، 17. 15 + 17 = 32 ، حتى تكون إجابتك صحيحة. آمن!
الطريقة 2 من 6: اطرح أعدادًا صحيحة صغيرة
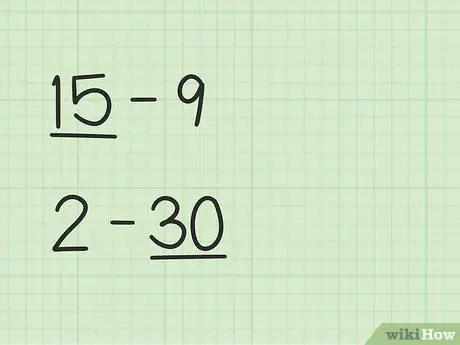
الخطوة 1. أوجد العدد الأكبر
سيكون للمسائل مثل 15 -9 طريقة مختلفة عن 2 - 30.
- في الأسئلة من 15 إلى 9 ، الرقم الأول ، 15 ، أكبر من الرقم الثاني ، 9.
- في الأسئلة من 2 إلى 30 ، الرقم الثاني ، 30 ، أكبر من الرقم الأول ، 2.
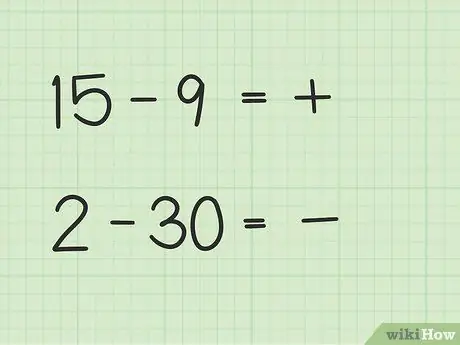
الخطوة الثانية: حدد ما إذا كانت إجابتك إيجابية أم سلبية
إذا كان الرقم الأول أكبر ، تكون الإجابة موجبة. إذا كان الرقم الثاني أكبر ، تكون الإجابة سالبة.
- في السؤال الأول ، 15-9 ، تكون إجابتك موجبة لأن الرقم الأول أكبر من الرقم الثاني.
- في السؤال الثاني ، 2 - 30 ، إجابتك سالبة لأن الرقم الثاني أكبر من الرقم الأول.
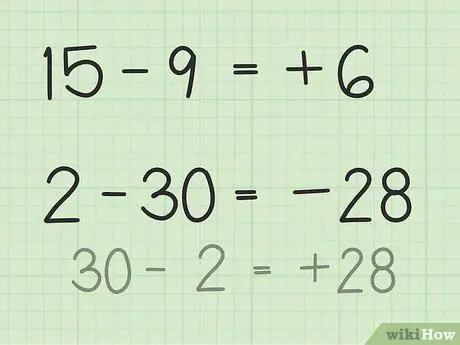
الخطوة الثالثة. أوجد الفرق بين عددين
لطرح رقمين ، عليك تخيل الفرق بين العددين وحساب الأرقام بينهما.
- للأسئلة من 15 إلى 9 ، تخيل كومة من 15 من رقائق البوكر. تخلص من 9 رقائق و 6 فقط. لذا ، 15 - 9 = 6. يمكنك أيضًا تخيل خط أرقام. فكر في الأرقام من 1 إلى 15 ، ثم تجاهل أو أعد 9 وحدات حتى تحصل على 6.
- بالنسبة للأسئلة من 2 إلى 30 ، فإن أسهل طريقة لحل ذلك هي عكس الرقم وجعل النتيجة سالبة بعد الطرح. إذن ، 30 - 2 = 28 ، لذا فإن الفرق بين 28 و 30 هو 2. الآن ، اجعل النتيجة سالبة لأنك حددت بالفعل أن الإجابة سالبة لأن الرقم الثاني أكبر من الرقم الأول. إذًا 2-30 = -28.
طريقة 3 من 6: طرح الكسور العشرية
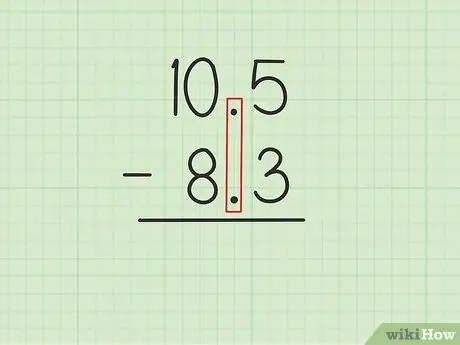
الخطوة 1. اكتب الرقم الأكبر على الرقم الأصغر مع محاذاة الفواصل العشرية
لنفترض أنك تريد حل المسائل التالية: 10 ، 5 - 8 ، 3. اكتب 10 ، 5 على 8 ، 3 بحيث تكون الفاصلة العشرية للعددين متوازية. ، 5 من 10 ، 5 يجب أن يكون أعلى مباشرة ، 3 من 8 ، 3 و 0 من 10 ، 5 يجب أن يكون أعلى من 8 من 8 ، 3.
إذا كانت لديك مشكلة لأن الرقمين لا يشتملان على نفس الرقم بعد الفاصلة العشرية ، فاكتب 0 في الفراغ حتى يتطابق مجموع الأرقام. على سبيل المثال ، المشكلة هي 5 ، 32 - 4 ، 2 ، يمكنك كتابتها على النحو 5 ، 32 - 4 ، 2 0. لن يغير هذا من قيمة الرقم الثاني ، ولكنه سيجعل طرح الرقمين أسهل.

الخطوة 2. اطرح الرقم العلوي في عمود العشرات من الرقم أدناه
في هذه الحالة ، عليك أن تطرح 3 من 5. 5 - 3 = 2 ، لذلك عليك أن تكتب 2 تحت 3 من 8 ، 3.
تأكد من وضع علامة عشرية في الإجابة ، بحيث تكون مكتوبة ، 2

الخطوة 3. اطرح الرقم الموجود أعلى عمود الوحدات من الرقم الموجود أسفله
عليك أن تطرح 8 من 0. اقترض 1 من جزء العشرات لتغيير 0 إلى 10 واطرح 10-8 للحصول على 2. يمكنك أيضًا عد 10-8 بدون استعارة لأنه لا توجد أرقام في عمود العشرات الثاني. اكتب الإجابة تحت 8 على يسار الفاصلة العشرية.

الخطوة 4. اكتب النتيجة النهائية
النتيجة النهائية هي 2، 2.

الخطوة 5. تحقق من عملك
إذا كنت تريد التأكد من صحة عملية الطرح العشري ، فكل ما عليك فعله هو جمع إجابتك مع الرقم الأصغر للحصول على الرقم الأكبر. 2 ، 2 + 8 ، 3 = 10 ، 5 ، لقد انتهيت.
طريقة 4 من 6: اطرح الكسور

الخطوة 1. قم بمحاذاة مقام الكسر وبسطه
افترض أنك تريد حل المسائل 13/10 - 3/5. اكتب المسألة بحيث يكون البسطان 13 و 3 والمقامان 10 و 5 متقابلان. يتم فصل هذين الرقمين بعلامة طرح. سيساعدك هذا على تصور المشكلة وحلها بسهولة أكبر.

الخطوة الثانية. أوجد المقام المشترك الأصغر
القاسم المشترك الأصغر هو أصغر عدد يمكن تقسيمه على رقمين. في هذا المثال ، عليك إيجاد أصغر مقام مشترك يقبل القسمة على 10 و 5. ستجد أن 10 هي أصغر مقام مشترك لكلا العددين لأن 10 يقبل القسمة على 10 و 5.
لاحظ أن المقام المشترك الأصغر لرقمين ليس دائمًا أحدهما. على سبيل المثال ، أصغر مقام مشترك لـ 3 و 2 هو 6 لأن 6 هو أصغر رقم يمكن قسمة رقمين
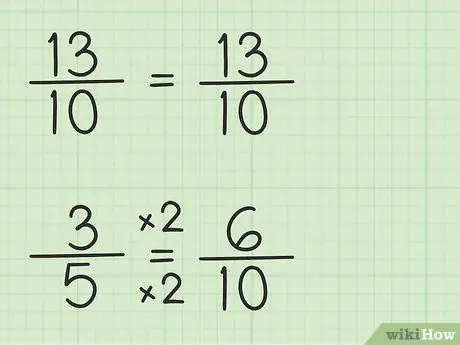
الخطوة 3. اكتب الكسور باستخدام نفس المقام
يمكن كتابة الكسر 13/10 بالطريقة نفسها لأن المقام هو 10 ، أصغر مقام مشترك ، وهو 10 ، في 1. ومع ذلك ، يجب إعادة كتابة الكسر 3/5 لأن المقام هو 5 ، أصغر مقام مشترك ، وهو 10 ، مضروبًا في 2. لذا يجب ضرب الكسر 3/5 في 2/2 ليصبح المقام 10 ، لذا 3/5 × 2/2 = 6/10. لقد وجدت الكسر المكافئ. 3/5 تعادل 6/10 على الرغم من أن 6/10 تسمح لك بطرح الرقم الأول ، 13/10.
اكتب سؤالاً جديداً مثل هذا: 13/10 - 6/10
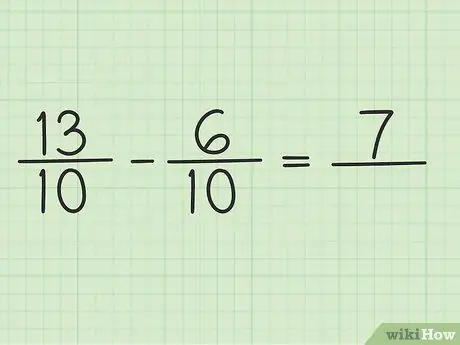
الخطوة 4. اطرح البسط إلى رقمين
فقط اطرح 13 - 6 لتصبح النتيجة 7. لا يمكنك تغيير مقام الكسر.
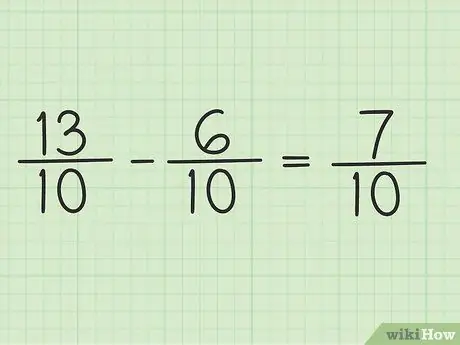
الخطوة 5. اكتب البسط الجديد فوق نفس المقام للحصول على النتيجة النهائية
البسط الجديد هو 7. كلا الكسرين مقامه 10. نتيجتك النهائية هي 7/10.
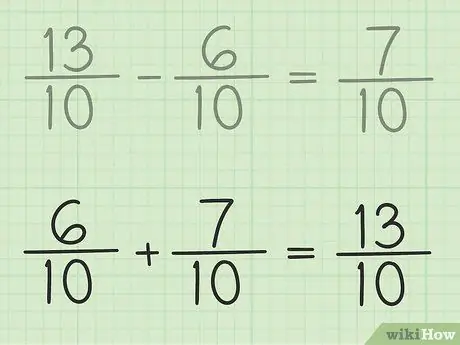
الخطوة 6. تحقق من عملك
إذا كنت تريد التأكد من أنك تطرح الكسر بشكل صحيح ، فما عليك سوى جمع إجابتك والكسر الأصغر بحيث تكون النتيجة كسرًا أكبر. 7/10 + 6/10 = 13/10. انتهى.
الطريقة 5 من 6: طرح الكسور من الأعداد الصحيحة

الخطوة الأولى. اكتب المشكلة
على سبيل المثال ، افترض أنك تريد حل المشكلة التالية: 5 -. اكتبه.
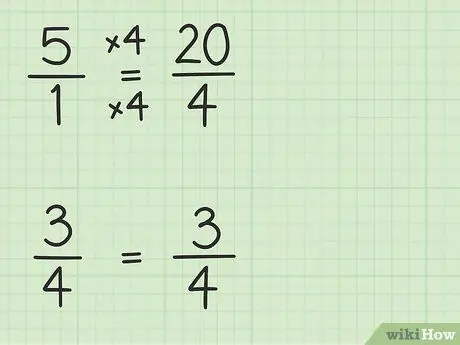
الخطوة الثانية. تحويل الأعداد الصحيحة إلى كسور لها نفس مقام الكسور الأخرى
ستحول 5 إلى كسر مقامه 4 لتتمكن من طرح عددين. لذلك عليك التفكير في 5 على أنها كسر 5/1. بعد ذلك ، يمكنك ضرب بسط ومقام الكسر الجديد في 4 لجعل مقامات العددين متماثلة. إذن 5/1 × 4/4 = 20/4. هذا الكسر يساوي 5 ، لكنه يسمح لك بطرح عددين.
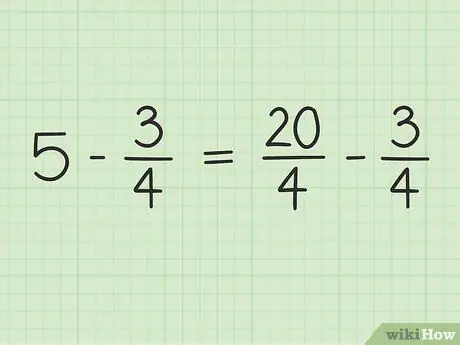
الخطوة 3. أعد كتابة المشكلة
يمكن كتابة المشكلة الجديدة على النحو التالي: 20/4 - 3/4.
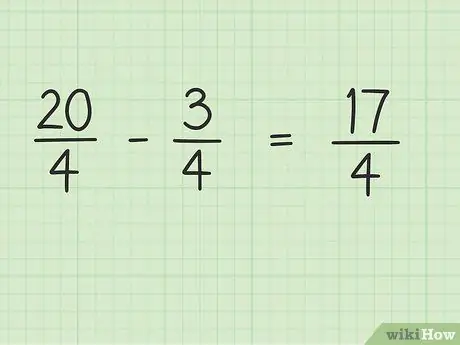
الخطوة 4. اطرح بسط الكسر ، بينما يبقى المقام كما هو
الآن ، اطرح 20 في 3 للحصول على النتيجة النهائية. 20-3 = 17 ، إذن 17 هو البسط الجديد. يمكنك ترك المقام كما هو.
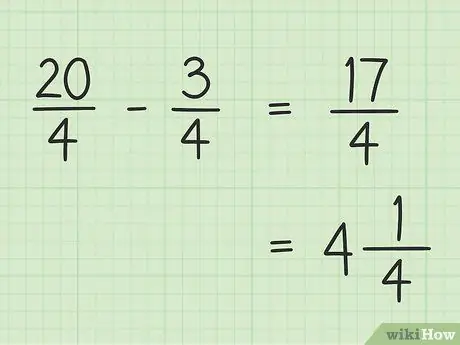
الخطوة 5. اكتب النتيجة النهائية
نتيجتك النهائية هي 17/4. إذا كنت تريد كتابته في صورة عدد كسري ، فاقسم 17 على 4 بحيث تكون النتيجة 4 والباقي 1 ، بحيث يكون 17/4 النهائي الخاص بك يساوي 4.
طريقة 6 من 6: طرح المتغيرات
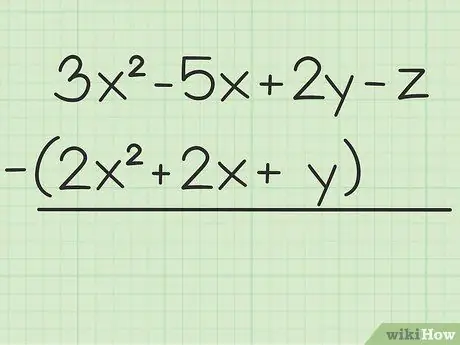
الخطوة الأولى. اكتب المشكلة التي تريد حلها
على سبيل المثال السؤال التالي: 3x2 - 5x + 2y - z - (2x2 + 2x + ص). اكتب المجموعة الأولى من المتغيرات على الثانية.
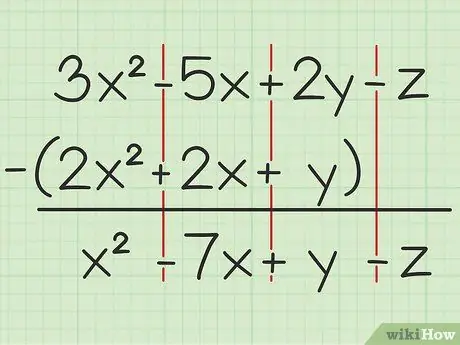
الخطوة 2. اطرح نفس المتغيرات
إذا واجهت متغيرًا ، فيمكنك فقط إضافة أو طرح نفس المتغير والذي تتم كتابته بنفس الدرجة من التربيع. هذا يعني أنه يمكنك طرح 4x2 من 7x2، لكن لا يمكن طرح 4x من 4y. لذلك ، يمكنك تقسيم المشكلة على النحو التالي:
- 3x2 - 2x2 = س2
- -5 س - 2 س = -7 س
- 2 ص - ص = ص
- -z - 0 = -z
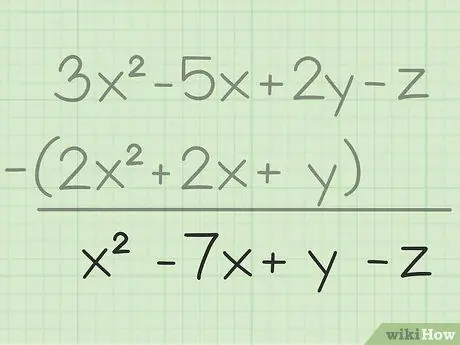
الخطوة 3. اكتب النتيجة النهائية الخاصة بك
لقد قمت بطرح جميع المتغيرات نفسها ، كل ما عليك فعله هو كتابة النتيجة النهائية التي ستحتوي على جميع المتغيرات التي طرحتها. ها هي النتيجة النهائية:






