المصفوفة هي ترتيب مستطيل من الأرقام أو الرموز أو التعبيرات في الصفوف والأعمدة. لضرب مصفوفة ، يجب أن تضرب العناصر (أو الأرقام) الموجودة في الصف الأول من المصفوفة في العناصر الموجودة في الصف الثاني من المصفوفة وتجمع حاصل الضرب. يمكنك ضرب المصفوفات ببضع خطوات سهلة تتطلب جمع النتائج وضربها ووضعها بشكل صحيح.
خطوة
الخطوة الأولى: تأكد من أن المصفوفات قابلة للضرب
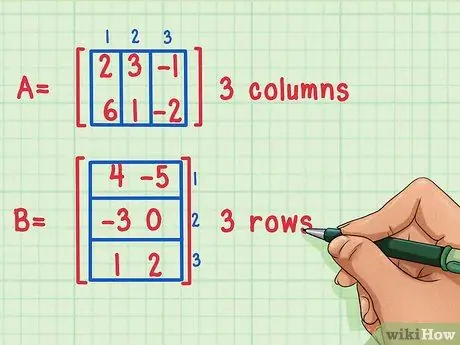
يمكنك فقط ضرب المصفوفة إذا كان عدد أعمدة المصفوفة الأولى يساوي عدد صفوف المصفوفة الثانية.
يمكن ضرب هذه المصفوفات لأن المصفوفة الأولى ، المصفوفة A ، بها 3 أعمدة ، بينما المصفوفة الثانية ، المصفوفة B ، بها 3 صفوف
الخطوة 2. حدد أبعاد حاصل ضرب المصفوفة
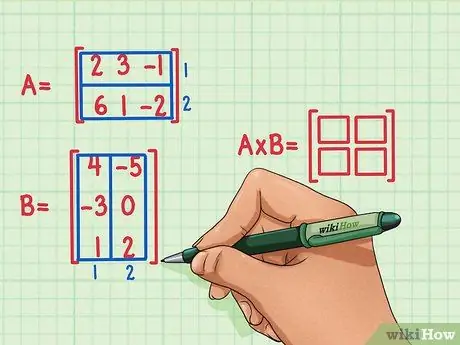
قم بإنشاء مصفوفة جديدة فارغة ، والتي ستحدد أبعاد حاصل ضرب المصفوفتين. المصفوفة التي تمثل حاصل ضرب المصفوفة A والمصفوفة B سيكون لها نفس عدد الصفوف مثل المصفوفة الأولى وعدد الأعمدة نفسه مثل المصفوفة الثانية. يمكنك رسم مربعات فارغة لإظهار عدد الصفوف والأعمدة في هذه المصفوفة.
- تحتوي المصفوفة A على صفين ، وبالتالي فإن نتيجة ضرب المصفوفة ستحتوي على صفين.
- تحتوي المصفوفة B على عمودين ، وبالتالي فإن نتيجة ضرب المصفوفة ستحتوي على عمودين.
- سيكون ناتج حاصل ضرب المصفوفة صفين وعمودين.
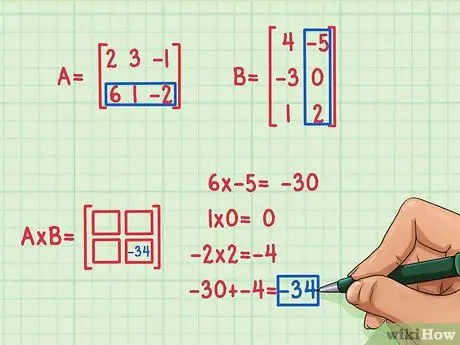
الخطوة الثالثة. ابحث عن نتيجة حاصل الضرب النقطي الأول
للعثور على نتيجة حاصل الضرب النقطي الأول ، يجب ضرب العنصر الأول في الصف الأول في العنصر الأول في العمود الأول ، والعنصر الثاني في الصف الأول في العنصر الثاني في العمود الأول ، والعنصر الثالث في الصف الأول بواسطة العنصر الثالث في العمود الأول. ثم اجمع نتائج الضرب لتجدها حاصل الضرب النقطي (نقطة).
لنفترض أنك قررت أولاً حساب العناصر في الصف الثاني والعمود الثاني (أسفل اليمين) من حاصل ضرب المصفوفة. إليك كيف تفعل ذلك:
- 6 × -5 = -30
- 1 × 0 = 0
- -2 × 2 = -4
- -30 + 0 + (-4) = -34
-
نتيجة حاصل الضرب القياسي هي -34 وهذه النتيجة مكتوبة في أسفل يمين حاصل ضرب المصفوفة.
عندما تضرب مصفوفة ، سيتم كتابة حاصل الضرب النقطي في موضع صف المصفوفة الأولى وموضع عمود المصفوفة الثانية. على سبيل المثال ، عندما تعرف حاصل الضرب القياسي للصف السفلي من المصفوفة أ والعمود الأيمن من المصفوفة ب ، فإن الإجابة ، -34 ، تكتب في الصف السفلي والعمود الأيمن من حاصل ضرب المصفوفة
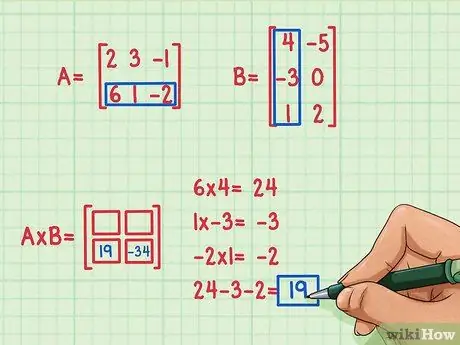
الخطوة 4. ابحث عن نتيجة حاصل الضرب النقطي الثاني
افترض أنك تريد إيجاد الحد الموجود أسفل يسار حاصل ضرب المصفوفة. للعثور على هذا الحد ، تحتاج فقط إلى ضرب العناصر الموجودة في الصف السفلي من المصفوفة الأولى في العناصر الموجودة في العمود الأول من المصفوفة الثانية ثم جمعها. استخدم نفس طريقة ضرب الصف الأول والعمود - ابحث مرة أخرى المنتج النقطي (لا) له.
- 6 × 4 = 24
- 1 × (-3) = -3
- (-2) × 1 = -2
- 24 + (-3) + (-2) = 19
- نتيجة حاصل الضرب القياسي هي -19 وهذه النتيجة مكتوبة في أسفل يسار حاصل ضرب المصفوفة.
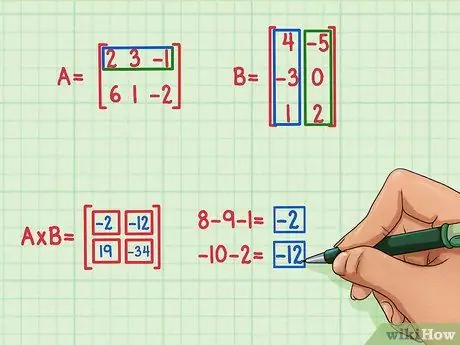
الخطوة 5. ابحث عن حاصل الضرب النقطي الآخرين
للعثور على المصطلح في أعلى يسار حاصل ضرب المصفوفة ، ابدأ بإيجاد حاصل الضرب القياسي للصف العلوي من المصفوفة A والعمود الأيسر من المصفوفة ب وإليك كيفية القيام بذلك:
- 2 × 4 = 8
- 3 × (-3) = -9
- (-1) × 1 = -1
- 8 + (-9) + (-1) = -2
-
نتيجة حاصل الضرب القياسي هي -2 وهذه النتيجة مكتوبة في أعلى يسار حاصل ضرب المصفوفة.
للعثور على المصطلح في الجزء العلوي الأيمن من حاصل ضرب المصفوفة ، ابحث فقط عن حاصل الضرب النقطي للصف العلوي من المصفوفة A والعمود الأيمن من المصفوفة ب. وإليك كيفية القيام بذلك:
- 2 × (-5) = -10
- 3 × 0 = 0
- (-1) × 2 = -2
- -10 + 0 + (-2) = -12
- حاصل الضرب القياسي هو -12 وهذه النتيجة مكتوبة في أعلى يمين حاصل ضرب المصفوفة.
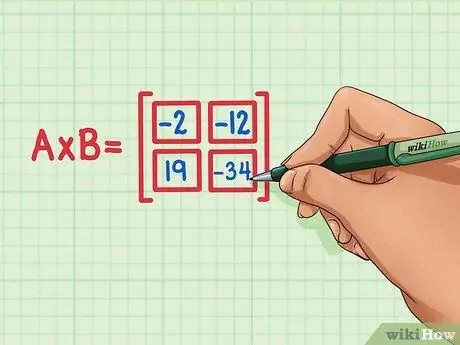
الخطوة 6. تأكد من أن حاصل الضرب النقطي الأربعة في المكان الصحيح في حاصل ضرب المصفوفة
يجب أن يكون الرقم 19 في أسفل اليسار ، و -34 في أسفل اليمين ، و -2 في أعلى اليسار ، و -12 في أعلى اليمين.
نصائح
- يمكن أن يؤدي استخدام مقاطع الخط ، وعدم استخدام الخطوط ، إلى إعطاء إجابة خاطئة. إذا كان الخط الذي يمثل صفًا يتطلب امتدادًا لعبور العمود ، فقم بإطالة العمود! هذا مجرد أسلوب مرئي لتسهيل معرفة الصفوف والأعمدة التي يجب استخدامها للعمل مع كل عنصر من عناصر المنتج.
- سينتج حاصل ضرب المصفوفتين عدد الصفوف يساوي عدد صفوف المصفوفة الأولى وعدد الأعمدة الذي يساوي عدد أعمدة المصفوفة الثانية.
- اكتب مجموعك. يتضمن ضرب المصفوفات الكثير من العمليات الحسابية ومن السهل جدًا الانحراف عن المسار ونسيان الرقم الذي تقوم بضربه.
