كيفية حساب متوسط السرعة: 12 خطوة (بالصور)

2024 مؤلف: Jason Gerald | [email protected]. آخر تعديل: 2024-02-01 14:11

كل ما تحتاجه لحساب متوسط السرعة هو الإزاحة الكلية. أو تغيير الموقف والوقت الإجمالي. تذكر أن السرعة تحسب أيضًا اتجاه الجسم وسرعته ، لذا قم بتضمين اتجاه في إجابتك ، مثل "الشمال" أو "الأمام" أو "اليسار". إذا كانت مشكلة حساب السرعة الخاصة بك تتضمن أيضًا تسريعًا ثابتًا ، فيمكنك تعلم طريقة سريعة للعثور على الإجابة بشكل أسهل.

خطوة

طريقة 1 من 2: حساب متوسط سرعة الإزاحة والوقت

الخطوة 1. تذكر أن السرعة تتضمن كلاً من سرعة الجسم واتجاهه

تصف السرعة المعدل الذي يتغير به موضع الكائن. هذا لا يتعلق فقط بمدى سرعة تحرك الجسم ، ولكن أيضًا مع اتجاهه. "100 متر في الثانية جنوبًا" قيمة سرعة مختلفة عن "100 متر في الثانية باتجاه الشرق".

• تسمى الكميات التي لها اتجاه كميات متجهة. يمكن تمييز هذه الكمية عن كمية بلا اتجاه تسمى كمية قياسية عن طريق كتابة سهم فوق المتغير. على سبيل المثال ، يمثل الرمز v المعدل ، بينما يمثل الرمز v ^→ يمثل السرعة أو السرعة + الاتجاه. يمثل الترميز v المستخدم في هذه المقالة السرعة.
• في المسائل العلمية ، يجب استخدام العدادات أو الوحدات المترية الأخرى للتعبير عن المسافة ، بينما للأغراض اليومية يمكنك استخدام أي وحدة تريدها.

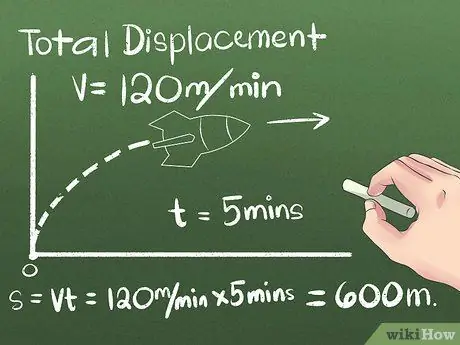
الخطوة 2. أوجد قيمة الإزاحة الإجمالية

الإزاحة هي التغيير في موضع الكائن ، أو المسافة والاتجاه بين نقطتي البداية والنهاية. يمكن إهمال الاتجاه الذي يتحرك فيه الكائن قبل الوصول إلى موضعه النهائي ، لأنه يتم أخذ المسافة بين نقطتي البداية والنهاية فقط في الاعتبار. في المثال الأول ، سنستخدم جسمًا يتحرك بسرعة ثابتة في اتجاه واحد:

• لنفترض أن صاروخًا يتحرك شمالًا لمدة 5 دقائق بسرعة ثابتة تبلغ 120 مترًا في الدقيقة. لحساب الموضع النهائي ، استخدم الصيغة s = vt ، أو استخدم التفكير العملي لحساب المسافة التي يقطعها الصاروخ بعد ذلك (5 دقائق) (120 مترًا / دقيقة) = 600 متر شمالا من نقطة البداية.
• بالنسبة للمسائل التي تتضمن تسارعًا ثابتًا ، يمكنك حلها باستخدام s = vt + at²، أو استخدم الطريقة القصيرة الموضحة في قسم آخر للعثور على الإجابة.

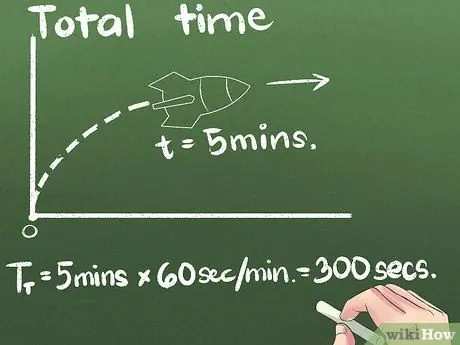
الخطوة الثالثة. أوجد إجمالي الوقت المنقضي

في مثالنا ، يتحرك الصاروخ للأمام لمدة 5 دقائق. يمكنك التعبير عن متوسط السرعة في أي وحدة زمنية ، ولكن الثانية هي الوحدة القياسية العلمية الدولية. سنقوم بتغيير وحدات الثواني في هذا المثال: (5 دقائق) × (60 ثانية / دقيقة) = 300 ثانية.

حتى في المسائل العلمية ، إذا كان السؤال يستخدم الساعة أو وحدة زمنية أكبر ، فسيكون من الأسهل حساب السرعة أولاً ، ثم تحويل الإجابة النهائية إلى متر / ثانية

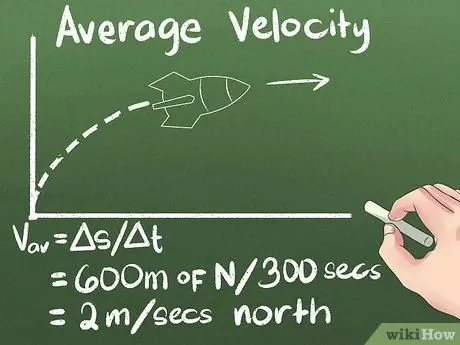
الخطوة 4. احسب السرعة المتوسطة كإزاحة بمرور الوقت

إذا كنت تعرف المسافة التي يتحرك بها جسم ما ، والوقت الذي سيستغرقه للوصول إليه ، فستعرف مدى سرعة تحركه. في المثال الذي نستخدمه ، متوسط سرعة الصاروخ هو (600 متر شمالًا) / (300 ثانية) = 2 متر / الثانية شمال.

• تذكر تضمين اتجاه (مثل "الجبهة" أو "الشمال").
• في الصيغة الخامس_av = ق / Δt. يعني رمز دلتا "التغيير" ، لذلك يعني s / Δt "التغيير في المركز خلال فترة زمنية."
• يمكن كتابة متوسط السرعة بالصيغة v_av، أو على شكل حرف v مع خط أفقي فوقه.

الخطوة 5. حل مشاكل أكثر تعقيدًا

إذا غير كائن ما اتجاهه أو سرعته ، فلا تشوش. لا يزال متوسط السرعة محسوبًا "فقط" من إجمالي الإزاحة والوقت الإجمالي. يمكنك تجاهل ما يحدث بين نقطتي البداية والنهاية. فيما يلي بعض الأمثلة على جسم يسافر بنفس الإزاحة والوقت الإجمالي ، وبالتالي ، نفس متوسط السرعة:

• تمشي آنا غربًا بسرعة 1 متر / ثانية لمدة ثانيتين ، ثم تسارعت فجأة إلى 3 أمتار / ثانية وتواصل المشي غربًا لمدة ثانيتين. الإزاحة الكلية (1 م / ث غربًا) (2 ث) + (3 م / ث غربًا) (2 ث) = 8 أمتار غربًا. الوقت الإجمالي 2 ثانية + 2 ثانية = 4 ثوان. إذن ، متوسط السرعة 8 أمتار غربًا / 4 ثوانٍ = 2 متر / الثانية غرب.

• يمشي بارت غربًا بسرعة 5 أمتار / ثانية لمدة 3 ثوانٍ ، ثم يستدير ويمشي شرقًا بسرعة 7 أمتار / ثانية لمدة ثانية واحدة. يمكننا التفكير في الحركة باتجاه الشرق على أنها "حركة سالبة باتجاه الغرب" وبالتالي فإن إجمالي الإزاحة = (5 أمتار / ثانية غربًا) (3 ثوانٍ) + (-7 م / ث غربًا) (1 ثانية) = 8 أمتار. الوقت الإجمالي = 4 ثوان. متوسط السرعة = 8 أمتار غربًا / 4 ثوانٍ = 2 متر / الثانية غرب.

• سارت شارلوت شمالًا مترًا واحدًا ثم سارت غربًا مسافة ٨ أمتار ، ثم سارت جنوباً مترًا واحدًا. الوقت المستغرق لإكمال الرحلة بأكملها هو 4 ثوانٍ. ارسم المخطط على قطعة من الورق ، وسترى أن نقطة النهاية هي 8 أمتار غرب نقطة البداية ، إذن هذه القيمة هي الإزاحة. الوقت الإجمالي الذي يستغرقه الأمر هو 4 ثوانٍ ، لذا فإن متوسط السرعة هو 8 أمتار غربًا / 4 ثوانٍ = 2 متر / الثانية غرب.

  طريقة 2 من 2: حساب متوسط السرعة للتسارع الثابت

  

  الخطوة 1. ضع في اعتبارك السرعة الابتدائية والعجلة الثابتة

  لنفترض أن مشكلتنا هي "دراجة تتحرك إلى اليمين بسرعة 5 م / ث ، بعجلة ثابتة 2 م / ث². إذا تحركت هذه الدراجة لمدة 5 ثوان ، فما متوسط سرعتها؟"

  إذا كانت الوحدة "متر / ثانية²"لإرباكك ، اكتبها كـ" متر / ثانية / ثانية "أو" متر لكل ثانية في الثانية ". يعني التسارع البالغ 2 متر / ثانية / ثانية أن السرعة تزيد بمقدار 2 متر في الثانية كل ثانية.

  

  الخطوة 2. استخدم التسارع لإيجاد السرعة النهائية

  التسارع ، المشار إليه بالرمز أ ، هو معدل تغير السرعة (أو المعدل). تزداد السرعة بمعدل زيادة ثابت. يمكنك رسم جدول باستخدام التسارع لإيجاد السرعة في أوقات مختلفة خلال رحلة الدراجة. نحتاج إلى إنشاء هذا الجدول للعثور على نقطة نهاية المشكلة (عند t = 5 ثوانٍ) ، لكننا سننشئ جدولًا أطول لتسهيل فهم هذا المفهوم:

  • عند نقطة البداية (الوقت t = 0 ثانية) ، تتحرك الدراجة بسرعة 5 أمتار / ثانية.
  • بعد ثانية واحدة (t = 1) ، تتحرك الدراجة بسرعة 5 أمتار / ثانية + عند = 5 أمتار / ثانية + (2 متر / ثانية)²) (ثانية واحدة) = 7 متر / ثانية.
  • عند t = 2 ، تتحرك الدراجة إلى اليمين بسرعة 5+ (2) (2) = 9 أمتار / ثانية.
  • عند t = 3 ، تتحرك الدراجة إلى اليمين بسرعة 5+ (2) (3) = 11 مترًا / ثانية.
  • عند t = 4 ، تتحرك الدراجة إلى اليمين بسرعة 5+ (2) (4) = 13 مترًا / ثانية.
  • عند t = 5 ، تتحرك الدراجة إلى اليمين بسرعة 5+ (2) (5) = 15 مترا / ثانية.

  

  الخطوة 3. استخدم هذه الصيغة لإيجاد متوسط السرعة

  إذا و "فقط" إذا كان التسارع ثابتًا ، فإن متوسط السرعة سيكون مساويًا لمتوسط قيمة مجموع السرعات النهائية والمبدئية. (الخامس_F + v_أنا)/2. لمثالنا أعلاه ، السرعة الابتدائية للدراجة هي v_أنا 5 أمتار / ثانية. بعد الحساب ، تكون السرعة النهائية v_F 15 مترا / ثانية. بجمع هاتين القيمتين معًا ، نحصل على (15 مترًا / ثانية + 5 مترًا / ثانية) / 2 = (20 مترًا / ثانية) / 2 = 10 متر / ثانية الاتجاه الصحيح.

  • تذكر تضمين الاتجاه ، في هذه الحالة "الحق".
  • يمكن كتابة هذا المصطلح كـ v₀ (السرعة في الوقت 0 ، أو السرعة الابتدائية) و v (السرعة النهائية).

  

  الخطوة 4. فهم صيغة متوسط السرعة بشكل حدسي

  لإيجاد السرعة المتوسطة ، يمكننا استخدام السرعة عند أي نقطة وإيجاد المتوسط لكل منهم. (هذا هو تعريف المتوسط.) بما أن هذا يتطلب حساب التفاضل والتكامل أو وقتًا لانهائيًا ، افهم هذه الصيغة بشكل حدسي أكثر. بدلاً من أخذ كل مرة ، احسب متوسط السرعة للنقطتين الزمنيتين وشاهد النتائج. توجد نقطة زمنية بالقرب من بداية الرحلة ، حيث تسير الدراجة ببطء ، ونقطة أخرى بالقرب من نقطة النهاية حيث تسير الدراجة بسرعة.

  

  الخطوة 5. اختبر النظرية البديهية

  استخدم الجدول أعلاه لتحديد السرعة في نقاط زمنية مختلفة. بعض الأزواج التي تلبي معاييرنا هي (t = 0 ، t = 5) ، (t = 1 ، t = 4) ، أو (t = 2 ، t = 3). يمكنك اختبار هذه الصيغة بقيم t بخلاف الأعداد الصحيحة أيضًا ، إذا كنت تريد ذلك.

  أيًا كان زوج النقاط الذي تختاره ، فإن متوسط السرعة في ذلك الوقت سيكون دائمًا كما هو. على سبيل المثال ، ((5 + 15) / 2) ، ((7 + 13) / 2) ، أو ((9 + 11) / 2) كلها تساوي 10 أمتار / ثانية إلى اليمين

  

  الخطوة 6. أكمل الشرح الحدسي

  إذا استخدمنا هذه الطريقة مع قائمة بكل مرة تستغرقها ، فسنستمر في حساب متوسط النصف الأول من الرحلة والنصف الثاني من الرحلة. الوقت المستغرق لتغطية كل نصف هو نفسه ، لذلك لا تضيع السرعة عندما ننتهي من العد.

  • نظرًا لأن أيًا من الزوجين سيعطي نفس النتيجة ، فإن متوسط هذه السرعات سيكون هو نفسه أيضًا من حيث القيمة. في مثالنا ، سرعة الكل "10 أمتار / ثانية إلى اليمين" وستظل 10 أمتار / ثانية إلى اليمين.
  • يمكننا إيجاد هذه القيمة بحساب متوسط أي زوج ، على سبيل المثال السرعات الابتدائية والنهائية. في مثالنا ، يتم الوصول إلى هذه السرعات عند t = 0 و t = 5 ، ويمكن حسابها باستخدام الصيغة أعلاه: (5 + 15) / 2 = 10 أمتار / ثانية إلى اليمين.

  

  الخطوة 7. فهم هذه الصيغة رياضيا

  إذا كنت تشعر براحة أكبر مع البراهين المكتوبة كصيغ ، فيمكنك البدء بصيغة لحساب المسافة المقطوعة بافتراض تسارع ثابت ، واشتقاق الصيغة من هناك:

  • ق = ت_أناt + at². (من الناحية الفنية ، s و t ، أو التغيير في الموضع والتغيير في الوقت ، ولكن سيتم فهمك أيضًا إذا كتبت s و t.)
  • متوسط السرعة_av تم تعريفه على أنه s / t ، لذا أدخل الصيغة في النموذج s / t.
  • الخامس_av = s / t = v_أنا + في
  • التسارع x الوقت يساوي التغير في السرعة الكلية ، أو v_F - الخامس_أنا. لذلك يمكننا استبدال "at" في الصيغة ، والحصول على:
  • الخامس_av = v_أنا + (v_F - الخامس_أنا).
  • تبسيط: v_av = v_أنا + v_F - الخامس_أنا = v_أنا + v_F = (الخامس_F + v_أنا)/2.

  نصائح

  • تختلف السرعة عن السرعة لأن السرعة كمية متجهة بينما السرعة كمية قياسية. تتضمن الكميات المتجهة كلاً من الاتجاه والمقدار ، بينما تتضمن الكميات العددية المقدار فقط.
  • إذا كان الكائن يتحرك في بُعد واحد ، مثل اليسار واليمين ، يمكنك استخدام رقم موجب لتمثيل اتجاه واحد (مثل اليمين) ورقم سالب لتمثيل اتجاه آخر (يسار). اكتب هذا الترميز في الجزء العلوي من صفحتك بحيث يكون واضحًا للأشخاص الذين يقرؤون عملك.