طالما أنك تعرف قياس الزاويتين الأخريين ، فمن السهل إيجاد الزاوية الثالثة في المثلث. ما عليك سوى طرح مجموع الزاويتين بمقدار 180 درجة. ومع ذلك ، هناك طرق أخرى يمكنك استخدامها لإيجاد الزاوية الثالثة للمثلث إذا كان شكل المشكلة مختلفًا قليلاً عن المعتاد. إذا كنت تريد معرفة كيفية إيجاد الزاوية الثالثة للمثلث ، فاتبع الدليل أدناه.
خطوة
طريقة 1 من 3: استخدام قياسات الزاويتين الأخريين
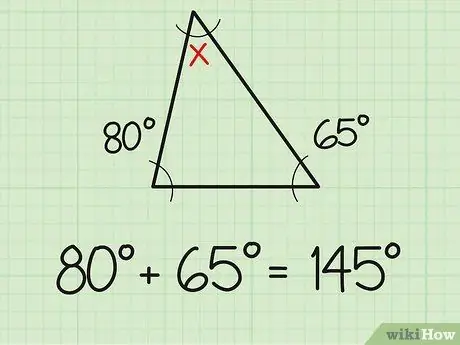
الخطوة 1. اجمع الزاويتين المعروفتين
إحدى الحقائق التي يجب أن تعرفها هي أن مجموع الزوايا الثلاث للمثلث يساوي دائمًا 180 درجة. لذا ، إذا كنت تعرف بالفعل قياس زاويتين في المثلث ، فإن إيجاد الزاوية الثالثة سيكون بسيطًا مثل القيام بمسائل الجمع والطرح البسيطة. أولًا ، اجمع قياس الزاويتين الذي تعرفه بالفعل. على سبيل المثال ، قياس زاويتين معروفتين 80 و 65 درجة. اجمع الاثنين معًا (80 + 65) ، وستحصل على 145 درجة.
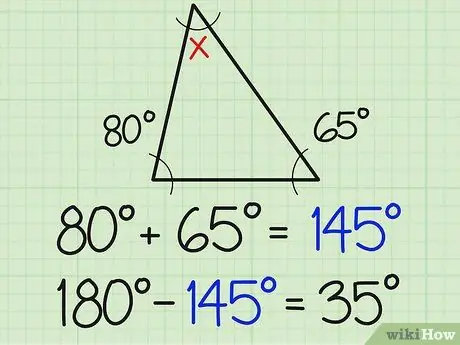
الخطوة 2. قسّم هذا الرقم على 180
مجموع زوايا المثلث الثلاث يساوي دائمًا 180 درجة. لذلك ، يجب أن تكون الزاوية الثالثة 180 عند إضافتها إلى مجموع المقياسين المعروفين للزاوية. في المثال أعلاه ، هذا يعني أن 180-154 = 35.
الخطوة 3. اكتب إجابتك
الآن لديك إجابة للزاوية الثالثة (في المثال 35 درجة). إذا كنت لا تزال في شك ، انظر بنفسك. اجمع الزوايا الثلاث معًا ، وستحصل على نتيجة 180. إذا لم تقم بذلك ، فإن حسابك خاطئ. في هذا المثال 80 + 65 + 35 = 180. إذا كان هذا صحيحًا ، فهذا يعني أنك قمت بحل المشكلة.
الطريقة 2 من 3: استخدام المتغيرات
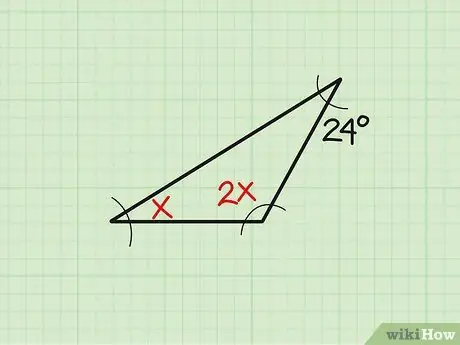
الخطوة الأولى. اكتب المشكلة
في بعض الأحيان ، يظهر حجم الزاوية الموجودة في شكل متغير. لنأخذ هذا المثال: "أوجد الزاوية" x "لمثلث إذا كانت الزوايا الثلاث قياسها" x "و" 2x "و 24 على التوالي." أولاً ، اكتب المشكلة.
الخطوة 2. اجمع كل قياسات الزاوية
المبدأ الذي يجب أن تتذكره يظل كما هو. لذا ، اجمع أولاً الزوايا الثلاث في المسألة ، وهي "x + 2x + 24 = 3x + 24".
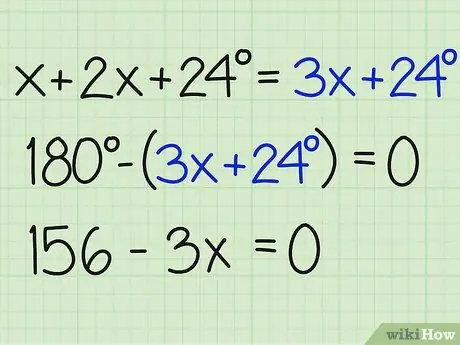
الخطوة 3. قسّم مجموع الزوايا على 180
الآن ، فرق هذا العدد بمقدار 180 درجة لإيجاد س ومعرفة إجابة المسألة. تأكد من إنهاء المعادلة بما يساوي صفرًا. إليك كيفية كتابتها:
- 180- (3 س + 24) = 0
- 180-3x-24 = 0
- 156-3x = 0
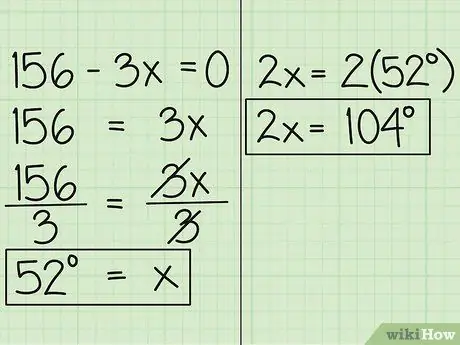
الخطوة 4. أوجد قيمة x
الآن ، انقل المتغير إلى الجانب الآخر من المعادلة ، وستحصل على 156 = 3x. ثم قسّم المعادلة على 3 ، لتحصل على x = 52. هذا يعني أن قياس الزاوية المعبر عنها في x هو 52 درجة. الزاوية الأخرى ، المُعبر عنها بـ 2x ، هي 52 درجة في 2 ، ما يساوي 104 درجات.
الخطوة 5. تحقق من نتائجك
إذا كنت تريد التأكد من صحة إجابتك ، فما عليك سوى جمع مقاييس الزوايا الثلاث التي وجدت الإجابة عليها بالفعل. إذا كانت النتيجة 180 ، فهذا يعني أن إجابتك صحيحة. في هذا المثال 52 + 104 + 24 = 180.
طريقة 3 من 3: استخدام طرق أخرى
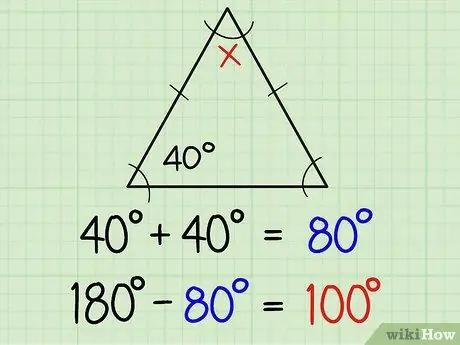
الخطوة 1. أوجد زوايا مثلث متساوي الساقين
مثلث متساوي الساقين ضلعان متساويان وزاويتان متساويتان. عادةً ما يتم تمييز ضلعين متساويين بخط صغير في منتصف الخط الجانبي ، مما يعني أن الزاويتين المتقابلتين على الخط هما نفس القياس. إذا كنت تعرف حجم إحدى الزوايا بالفعل ، فأنت تعرف الزاوية الأخرى تلقائيًا. فيما يلي شرح إضافي:
إذا كانت إحدى الزاويتين المتساويتين 40 درجة ، فإن الأخرى 40 درجة. بهذه الطريقة يمكنك إيجاد جميع الزوايا الثلاث مع الفرق بين مجموع 40 + 40 (أي 80) و 180 ، أو بعبارة أخرى 180-80 = 100
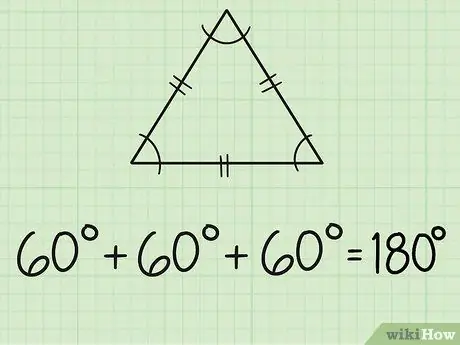
الخطوة الثانية: أوجد زوايا مثلث متساوي الأضلاع
مثلث متساوي الأضلاع له ثلاثة أضلاع متساوية وثلاث زوايا متساوية. عادة ما يتم تمييز كل جانب بخطين قصيرين في المنتصف. بما أن الزوايا الثلاث متساوية ، فهذا يعني أن قياس جميع الزوايا 60 درجة ، لأن 180/3 = 60.
الخطوة 3. أوجد الزاوية الثالثة في مثلث قائم الزاوية
لنفترض أنك حصلت على مثلث قائم الزاوية ، بإحدى الزوايا الحادة قياسها 30 درجة. بما أن المثلث قائم الزاوية ، فهذا يعني أن إحدى الزوايا ، وهي الزاوية القائمة ، يجب أن يكون قياسها 90 درجة. ثم استخدم مبدأ المثلث ، الفرق بين مجموع الزاويتين (90 + 30 = 120) في 180 ، ثم ستحصل على 180-120 = 60 درجة.
