- مؤلف Jason Gerald [email protected].
- Public 2023-12-16 10:53.
- آخر تعديل 2025-01-23 12:06.
تعد إضافة الكسور معرفة مفيدة جدًا. هذه المهارة سهلة التعلم والاستخدام عند العمل على حل مسائل الرياضيات من المرحلة الابتدائية إلى الثانوية. تشرح هذه المقالة كيفية إضافة الكسور حتى تتمكن من القيام بذلك في دقائق قليلة.
خطوة
الطريقة 1 من 2: جمع الكسور ذات المقام نفسه

الخطوة 1. تحقق من المقام (الرقم الموجود أسفل حاصل القسمة) لكل كسر
إذا كانت الأرقام متطابقة ، فأنت تجمع كسورًا بنفس المقام. إذا كانت المقامات مختلفة ، فاقرأ الطريقة الثانية.
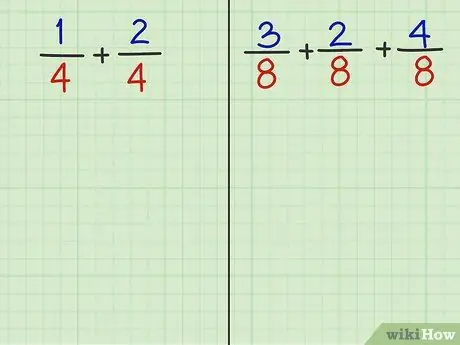
الخطوة 2. أجب عن السؤالين التاليين
من خلال قراءة الخطوة الأخيرة في هذه الطريقة ، يجب أن تكون قادرًا على جمع كسور السؤالين التاليين.
- المشكلة 1: 1/4 + 2/4
- المشكلة 2: 3/8 + 2/8 + 4/8
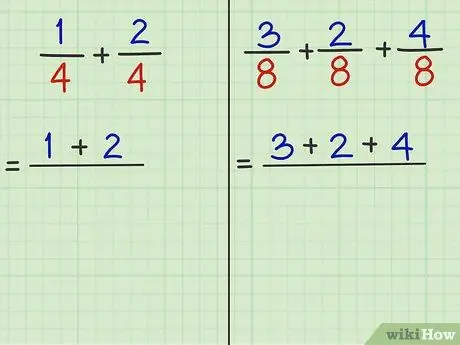
الخطوة الثالثة. اجمع البسط (الأرقام فوق القسمة) واجمعها
البسط هو الرقم الموجود فوق حاصل القسمة. بغض النظر عن عدد الكسور التي تريد جمعها ، يمكنك جمع البسط على الفور إذا كانت المقامات متطابقة.
- المشكلة 1: 1/4 + 2/4 هو الكسر المراد إضافته. "1" و "2" عبارة عن بسط. إذن ، 1 + 2 = 3.
- المشكلة 2: 3/8 + 2/8 + 4/8 هو الكسر المراد إضافته. "3" و "2" و "4" هي البسط. إذن ، 3 + 2 + 4 = 9.

الخطوة 4. حدد الكسر الجديد من المجموع
اكتب البسط الذي تم الحصول عليه في الخطوة 2. هذا الرقم هو بسط جديد. اكتب المقام ، وهو نفس العدد تحت منصف كل كسر. لا تحتاج إلى إجراء العمليات الحسابية إذا كانت المقامات متطابقة. هذا الرقم قاسم جديد ودائمًا ما يساوي المقام القديم عند جمع كسور لها نفس المقام.
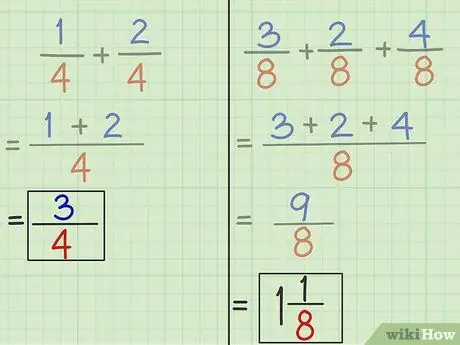
- المشكلة 1: 3 هو البسط الجديد و 4 هو المقام الجديد. وبالتالي ، فإن الإجابة على السؤال 1 هي 3/4. 1/4 + 2/4 = 3/4.
- المشكلة 2: 9 هو البسط الجديد و 8 هو المقام الجديد. إذن ، إجابة السؤال 2 هي 9/8. 3/8 + 2/8 + 4/8 = 9/8.
الخطوة 5. بسّط الكسور إذا لزم الأمر
لا تنس تبسيط الكسر الجديد لتبسيط الكتابة.
-
إذا كان البسط أكبر بدلاً من المقام مثل نتيجة إضافة المسألة 2 ، هذا يعني أننا نحصل على شهر كامل بعد تبسيط الكسر. اقسم البسط على المقام أو 9 على 8. النتيجة هي عدد صحيح 1 متبقي 1. اكتب أعداد صحيحة أمام الكسر والباقي يصبح بسط كسر جديد له نفس المقام.
9/8 = 1 1/8.
الطريقة 2 من 2: جمع الكسور ذات المقامات المختلفة

الخطوة 1. تحقق من المقام (الرقم الموجود أسفل حاصل القسمة) لكل كسر
إذا كانت المقامات مختلفة ، فأنت اجمع الكسور ذات القواسم المختلفة. اقرأ الخطوات التالية لأن عليك جعل المقامات متساوية قبل إضافة الكسور.
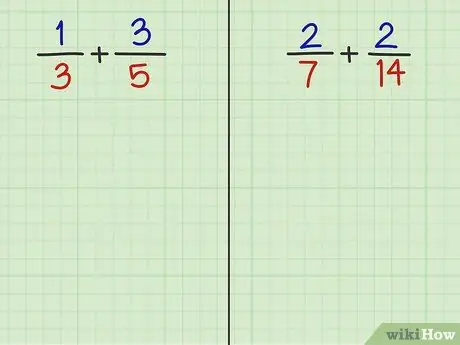
الخطوة 2. حل السؤالين التاليين
من خلال قراءة الخطوة الأخيرة في هذه الطريقة ، يجب أن تكون قادرًا على جمع كسور السؤالين التاليين.
- مشكلة 3: 1/3 + 3/5
- السؤال 4: 2/7 + 2/14

الخطوة 3. تطابق القواسم
للقيام بذلك ، اضرب مقامات الكسرين أعلاه. من الطرق السهلة لمعادلة المقامات ضرب مقامي الكسرين. إذا كان أحد المقامين مضاعفًا للآخر ، فابحث عن المضاعف المشترك الأصغر للمقامين.
-
مشكلة 3:
3 × 5 = 15. إذن ، المقام الجديد لكلا الكسرين هو 15.
-
المشكلة 4:
14 مضاعف للعدد 7. لذلك ، نحتاج فقط إلى ضرب 7 في 2 لنحصل على 14. وبالتالي ، فإن المقام الجديد لكلا الكسرين هو 14.

الخطوة 4. اضرب بسط الكسر الأول ومقامه في مقام الكسر الثاني
لا تغير هذه الخطوة قيمة الكسر ، لكن يبدو أن الكسر يتغير ليطابق المقام. تبقى القيمة الكسرية كما هي.
-
مشكلة 3:
1/3 × 5/5 = 5/15.
-
المشكلة 4:
في هذه المسألة ، علينا فقط ضرب الكسر الأول في 2/2 لنحصل على المقامات متساوية.
2/7 × 2/2 = 4/14

الخطوة 5. اضرب بسط الكسر الثاني ومقامه في مقام الكسر الأول
على غرار الخطوات المذكورة أعلاه ، لا نغير قيمة الكسر ، لكن يبدو أن الكسر يتغير لمعادلة المقام. تبقى القيمة الكسرية كما هي.
-
مشكلة 3:
3/5 × 3/3 = 9/15.
-
المشكلة 4:
لا نحتاج إلى ضرب الكسر الثاني لأن المقامان متماثلان.

الخطوة 6. اكتب الكسرين الجديدين بالترتيب
في هذه المرحلة ، لم نجمع الكسرين معًا ، رغم أننا نستطيع ذلك. في الخطوة أعلاه ، قمنا بضرب كل كسر في 1. والآن ، نريد التأكد من أن الكسور التي نريد جمعها لها نفس المقام.
-
مشكلة 3:
بدلًا من 1/3 + 3/5 ، يصبح الكسر 5/15 + 9/15
-
المشكلة 4:
بدلاً من 2/7 + 2/14 ، يصبح الكسر 4/14 + 2/14

الخطوة 7. اجمع بسط الكسرين معًا
البسط هو الرقم الموجود فوق حاصل القسمة.
-
مشكلة 3:
5 + 9 = 14. 14 هو البسط الجديد.
-
المشكلة 4:
4 + 2 = 6. 6 هو البسط الجديد.

الخطوة 8. اكتب المقام المشترك (في الخطوة 2) تحت البسط الجديد أو استخدم مقام الكسر مضروبًا في 1 لمعادلة المقام
-
مشكلة 3:
15 هو المقام الجديد.
-
المشكلة 4:
14 هو المقام الجديد.

الخطوة 9. اكتب بسطًا جديدًا ومقامًا جديدًا
-
مشكلة 3:
14/15 هل الجواب 1/3 + 3/5 =؟
-
المشكلة 4:
6/14 هل الجواب 2/7 + 2/14 =؟

الخطوة 10. تبسيط وتقليل الكسور
لتبسيط الكسور ، اقسم البسط والمقام على أكبر عامل مشترك بين العددين.
-
مشكلة 3:
14/15 لا يمكن تبسيطه.
-
المشكلة 4:
يمكن اختزال 6/14 إلى 3/7 بعد قسمة البسط والمقام على 2 باعتباره أكبر عامل مشترك بين 6 و 14.
نصائح
- قبل إضافة الكسور ، تأكد من أن المقامات متطابقة.
- لا تضيف القواسم. إذا كانت المقامات متطابقة ، فاستخدم الرقم كمقام بعد إضافة الكسور.
- إذا كنت تريد إضافة كسور بأرقام تتكون من أعداد صحيحة وكسور ، فحول هذه الأرقام إلى كسور واجمعها وفقًا للإرشادات أعلاه.






