- مؤلف Jason Gerald [email protected].
- Public 2023-12-16 10:53.
- آخر تعديل 2025-01-23 12:06.
هناك العديد من الأشكال المختلفة للأشكال المسطحة وهناك العديد من الأسباب التي قد تجعلك ترغب في حساب المساحة: من القيام بالواجب المنزلي إلى تقدير كمية الطلاء المطلوبة لإعادة طلاء غرفة المعيشة. لا تقلق ، لدى wikiHow الإجابة! ابدأ من الخطوة 1 أدناه لمعرفة كيفية حساب مساحة الشكل المستوي.
خطوة
طريقة 1 من 7: مربع ، مستطيل ومتوازي الأضلاع
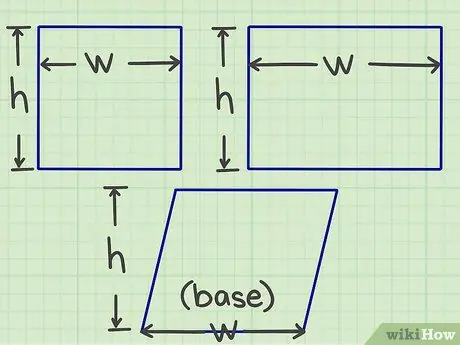
الخطوة 1. قياس الطول والعرض
ابدأ بقياس أو تحديد طول وعرض الشكل المسطح (أو بعبارة أخرى ، حجم كل جانب من الجانبين اللذين يلتقيان عند نقطة واحدة).
- بالنسبة إلى متوازي الأضلاع ، عليك إيجاد القاعدة والارتفاع ، لكن بعبارات بسيطة ، الفكرة هي نفسها الطول والعرض.
- في العالم الحقيقي ، قد تحتاج إلى قياسه بنفسك ، ولكن عندما يتعلق الأمر بأداء الواجب المنزلي ، فعادة ما يكون المعلم قد كتب بالفعل الأرقام مع صورة للشكل.
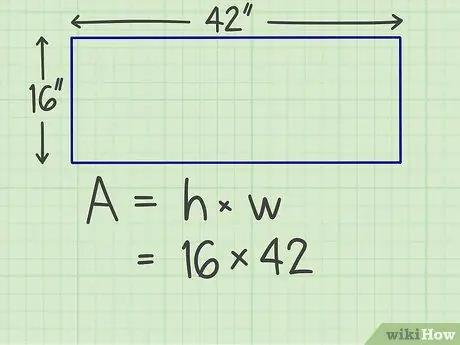
الخطوة 2. اضرب الجوانب
اضرب جانبًا في الآخر. على سبيل المثال ، افترض أن لديك مستطيلًا بعرض 16 بوصة وطوله 42 بوصة ، لذلك عليك حساب 16 × 42.
إذا كنت تحسب مساحة المربع (المربع سابقًا) ، فوفر الوقت عن طريق تربيع أحد أضلاعه باستخدام آلة حاسبة. إذا كان طول الجانب 4 أمتار ، فاضغط على المفتاح 4 ثم اضغط على المفتاح المربع في الآلة الحاسبة لعرض النتيجة. المربع يعني ضرب رقم في نفسه
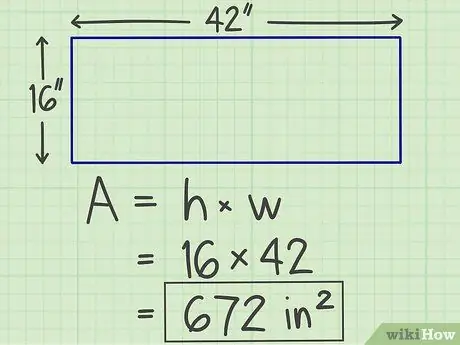
الخطوة 3. اكتب النتائج
الضرب الذي قمت به سابقًا سينتج رقمًا ، وهو مساحة المستوى الذي تحسبه ، بوحدة "المربع". وبالتالي ، تبلغ مساحة المستطيل الذي حسبناه سابقًا 672 بوصة مربعة.
في بعض الأحيان يتم كتابة هذه الوحدة المربعة أيضًا على أنها 2 صغيرة ترتفع قليلاً بعد اسم الوحدة (مثل قوى الكتابة)
طريقة 2 من 7: شبه منحرف
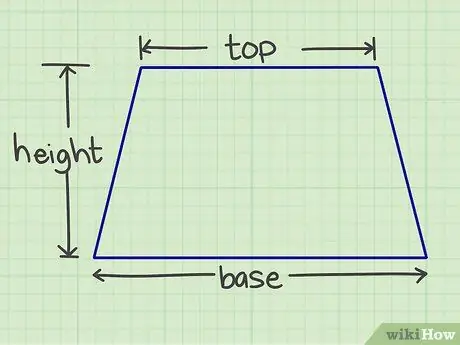
الخطوة 1. قم بقياس العدد المطلوب
سوف تحتاج إلى قياس القاعدة والسقف والارتفاع. القاعدة والسقف جانبان متوازيان ، بينما الارتفاع عبارة عن خط عمودي يربط بين الجانبين المتوازيين.
في العالم الحقيقي ، قد تحتاج إلى قياسه بنفسك ، ولكن عندما يتعلق الأمر بأداء الواجب المنزلي ، فعادة ما يكون المعلم قد كتب بالفعل الأرقام مع صورة للشكل
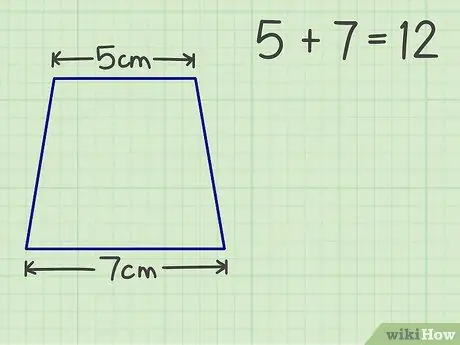
الخطوة 2. أضف الجانبين المتوازيين
على سبيل المثال ، لدينا سقف شبه منحرف 5 سم وقاعدة 7 سم. مجموع الضلعين المتوازيين هو 12.
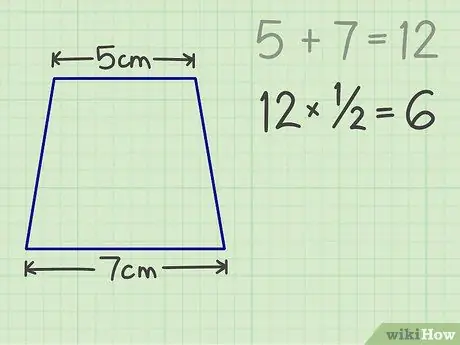
الخطوة 3. اضرب الرقم في 1/2 ، النتيجة هي 6
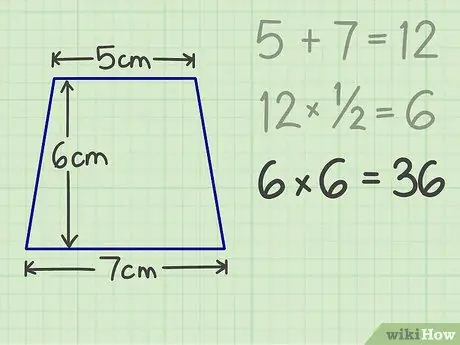
الخطوة 4. بعد ذلك اضرب الناتج في الارتفاع
على سبيل المثال ، إذا كان ارتفاع شبه منحرف 6 سم ، فإن النتيجة النهائية هي 36.
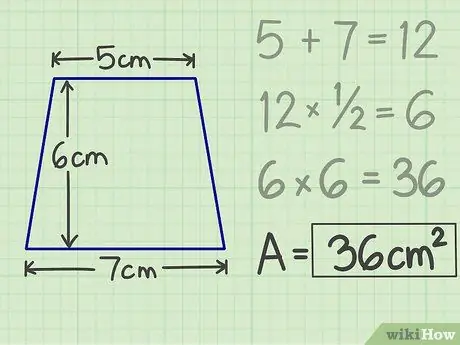
الخطوة 5. اكتب النتائج
سوف ينتج عن الضرب الذي قمت به سابقًا رقمًا ، أي مساحة شبه المنحرف. إذن ، بالنسبة لشبه منحرف بسقف 5 سم وقاعدته 7 سم وارتفاعه 6 سم ، فإن مساحته 36 سم مربع.
طريقة 3 من 7: الدائرة
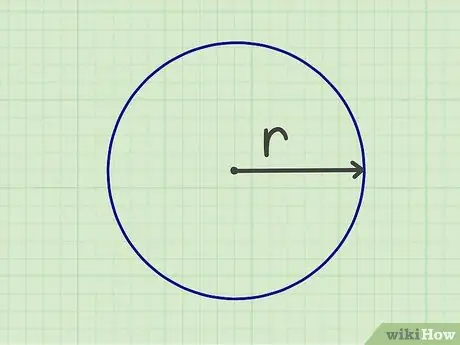
الخطوة 1. قياس نصف القطر
لتتمكن من حساب مساحة الدائرة ، عليك قياس نصف القطر. نصف القطر هو المسافة من مركز الدائرة إلى حافتها. يمكنك أيضًا قياس نصف القطر عن طريق قياس القطر (عرض الدائرة من الحافة إلى الحافة) ، ثم قسمة الرقم على اثنين.
في العالم الحقيقي ، قد تحتاج إلى قياسه بنفسك ، ولكن عندما يتعلق الأمر بأداء الواجب المنزلي ، فعادة ما يكون المعلم قد كتب بالفعل الأرقام مع صورة للشكل
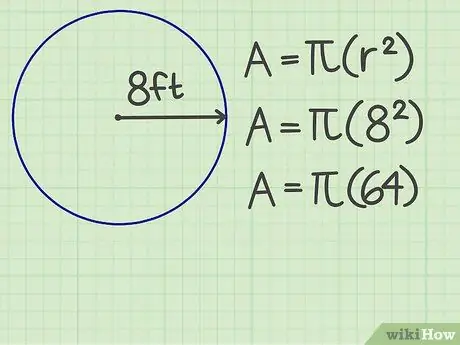
الخطوة 2. مربّع الأصابع
اضرب عدد أنصاف الأقطار في نفسه. على سبيل المثال ، يبلغ نصف قطر الدائرة 8 أقدام ، وبالتالي تكون النتيجة 64.
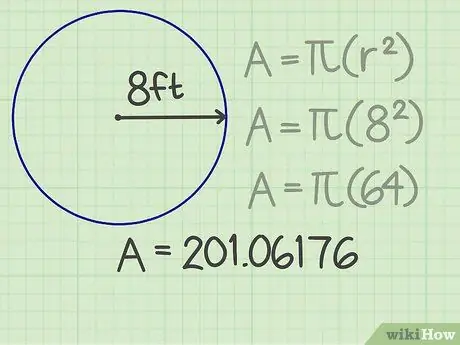
الخطوة 3. اضرب الناتج في pi
Pi (π) هو رقم مهم يستخدم في صيغ مختلفة. إذا كنت تستخدم آلة حاسبة ، فاضغط على مفتاح pi للحصول على نتائج دقيقة حقًا. بخلاف ذلك ، لتسهيل العمليات الحسابية ، يمكنك تقريب pi إلى بضعة أرقام بعد الفاصلة ، على سبيل المثال 3 ، 14159. عندما تضرب هذا الرقم في مربع نصف القطر ، تكون النتيجة 201 ، 06176.
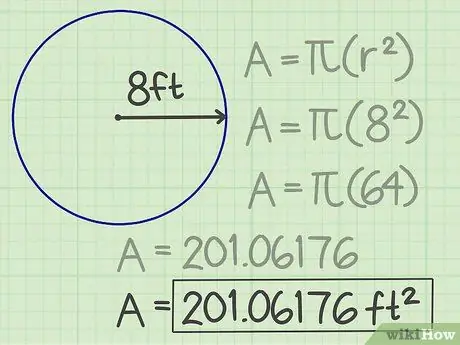
الخطوة 4. اكتب النتائج
العدد الذي تم الحصول عليه ، 06176 هو مساحة الدائرة. وبذلك تبلغ مساحتها 201.06176 قدم مربع.
طريقة 4 من 7: القطاع (جورينج)
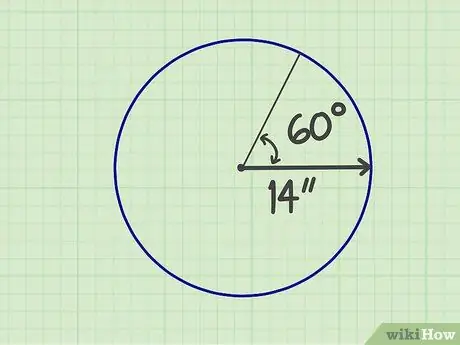
الخطوة 1. قم بقياس الأرقام المطلوبة
القطاع هو جزء من دائرة يتكون من نصف قطر وحافة ، بحيث يكون الشكل مثل المروحة. تحتاج إلى معرفة حجم نصف القطر ، والزاوية التي تتكون منها "المروحة". على سبيل المثال ، افترض أن نصف قطر قطاع ما 14 بوصة وزاوية 60 درجة.
في العالم الحقيقي ، قد تحتاج إلى قياسه بنفسك ، ولكن عندما يتعلق الأمر بأداء الواجب المنزلي ، فعادة ما يكون المعلم قد كتب بالفعل الأرقام مع صورة للشكل
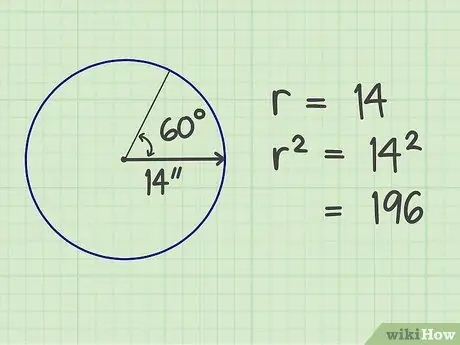
الخطوة 2. مربّع الأصابع
اضرب عدد أنصاف الأقطار في نفسه. والنتيجة هي 196 (14x14).

الخطوة 3. اضرب الناتج في باي
Pi (π) هو رقم مهم يستخدم في صيغ مختلفة. إذا كنت تستخدم آلة حاسبة ، فاضغط على مفتاح pi للحصول على نتائج دقيقة حقًا. بخلاف ذلك ، لتسهيل العمليات الحسابية ، يمكنك تقريب pi إلى بضعة أرقام بعد الفاصلة ، على سبيل المثال 3 ، 14159. إذا ضربت هذا الرقم في مربع نصف القطر ، فستكون النتيجة 615 ، 75164.

الخطوة 4. قسّم قياس الزاوية على 360
اقسم زاوية مروحة القطاع على 360 (قياس زاوية الدائرة الكاملة). بالنسبة للمثال أعلاه ، تكون النتيجة حوالي 0.166. إذا قمت بحسابها باستخدام آلة حاسبة ، فستكون النتيجة في الواقع أطول ومتكررة ، ولكن هنا يتم تقريبها لتسهيل الحساب.

الخطوة 5. اضرب هذا الرقم في الرقم السابق
اضرب الرقم الذي تحصل عليه بعد قسمة الزاوية على 360 ، في الرقم الذي حصلت عليه سابقًا بعد ضرب pi في مربع نصف القطر. بالنسبة للمثال أعلاه ، تكون النتيجة 102 ، 214 (بعد التقريب).
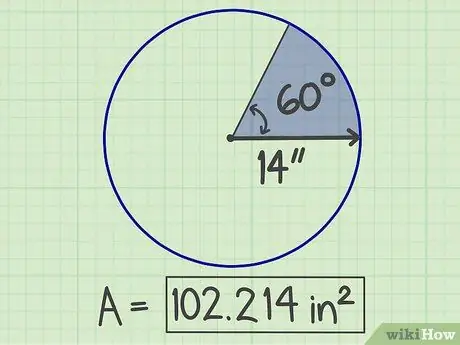
الخطوة 6. اكتب النتائج
الرقم الذي تم الحصول عليه هو مساحة القطاع ، وهي 102.214 بوصة مربعة.
طريقة 5 من 7: القطع الناقص
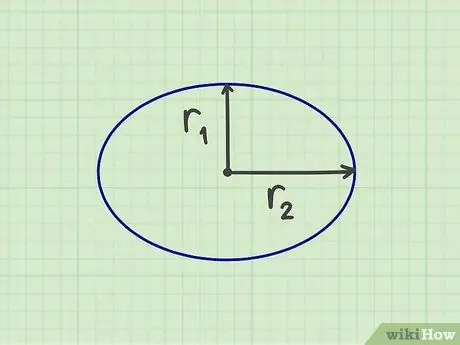
الخطوة 1. قم بقياس العدد المطلوب
لحساب مساحة القطع الناقص ، تحتاج إلى قياس "نصف قطر" ، أي نصف القطر القصير ونصف القطر الطويل ، وهو نصف عرض ونصف ارتفاع القطع الناقص. يمكنك أيضًا قياس نصف القطر القصير من مركز القطع الناقص إلى الجانب الأقصر ، ونصف القطر الطويل من مركز القطع الناقص إلى الجانب الأطول. يجب أن يشكل نصف القطر القصير زاوية قائمة على نصف القطر الطويل.
في العالم الحقيقي ، قد تحتاج إلى قياسه بنفسك ، ولكن عندما يتعلق الأمر بأداء الواجب المنزلي ، فعادة ما يكون المعلم قد كتب بالفعل الأرقام مع صورة للشكل
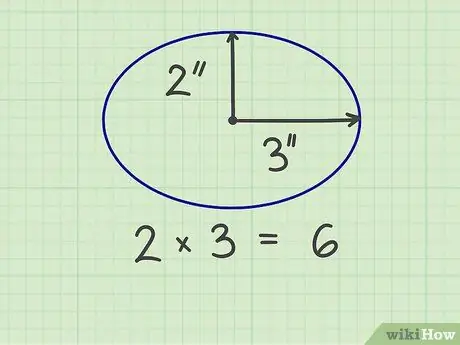
الخطوة 2. اضرب إصبعين
على سبيل المثال ، يبلغ عرض القطع الناقص 6 بوصات وارتفاعه 4 بوصات ، لذا يبلغ نصف القطر 3 بوصات و 2 بوصات. عندما يتم ضرب العددين ، تكون النتيجة 6 (3 × 2).

الخطوة 3. اضرب الناتج في pi
Pi (π) هو رقم مهم يستخدم في صيغ مختلفة. إذا كنت تستخدم آلة حاسبة ، فاضغط على مفتاح pi للحصول على نتائج دقيقة حقًا. بخلاف ذلك ، لتسهيل العمليات الحسابية ، يمكنك تقريب pi إلى بضعة أرقام بعد الفاصلة ، على سبيل المثال 3 ، 14159. عندما تضرب هذا الرقم في مربع نصف القطر ، تكون النتيجة 18 ، 84954.
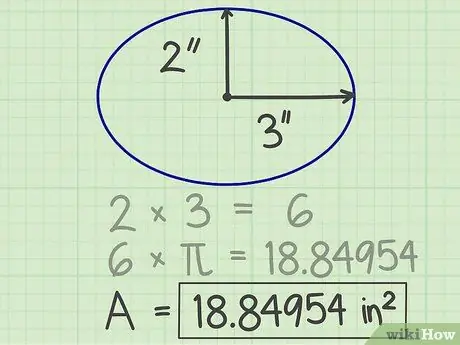
الخطوة 4. اكتب النتائج
الرقم الذي تم الحصول عليه من الحساب أعلاه هو مساحة القطع الناقص. في المثال أعلاه ، تبلغ مساحة القطع الناقص 18.84954 بوصة مربعة.
طريقة 6 من 7: المثلث
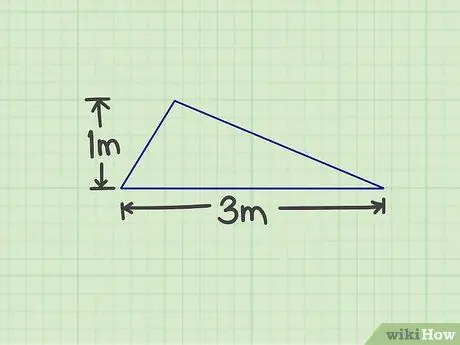
الخطوة 1. قم بقياس العدد المطلوب
تحتاج إلى قياس قاعدة المثلث وارتفاعه. يمكن أن يكون أي جانب من أضلاع المثلث هو القاعدة ، طالما يمكنك قياس الارتفاع. على سبيل المثال ، يوجد مثلث قاعدته 3 م وارتفاعه 1 م.
في العالم الحقيقي ، قد تحتاج إلى قياسه بنفسك ، ولكن عندما يتعلق الأمر بأداء الواجب المنزلي ، فعادة ما يكون المعلم قد كتب بالفعل الأرقام مع صورة للشكل
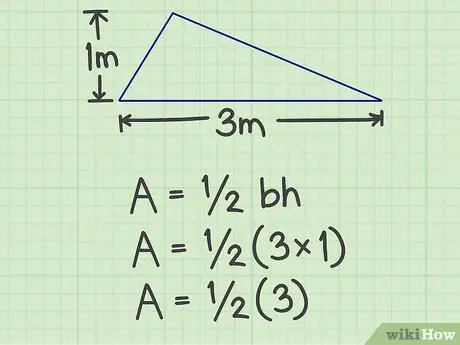
الخطوة 2. اضرب القاعدة في الارتفاع
بالنسبة للمثال أعلاه ، تكون النتيجة 3 (3x1).
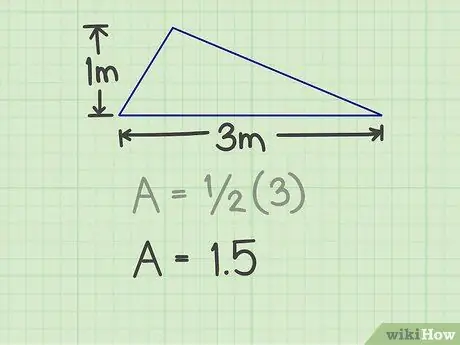
الخطوة 3. اضرب الناتج في 1/2
ينتج عن هذا الضرب الأعداد 1 ، 5.
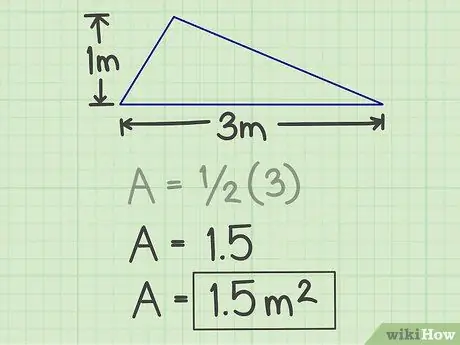
الخطوة 4. اكتب النتائج
الرقم الناتج عن الحساب أعلاه هو مساحة المثلث ، ومع المثال أعلاه ، تبلغ مساحته 1.5 متر مربع.
طريقة 7 من 7: البناء المسطح المعقد
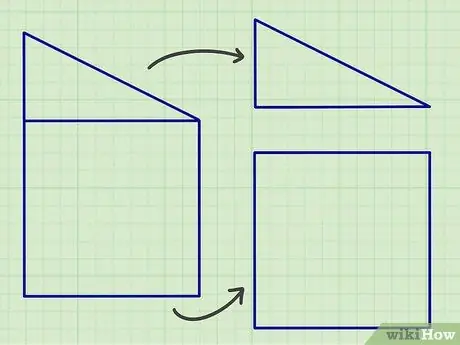
الخطوة 1. افصل الأشكال المستوية المعقدة إلى أجزاء تتكون من الأشكال الهندسية القياسية أعلاه
إذا كان ما تفعله واجبًا منزليًا ، فقد يكون من السهل تقسيم الشكل المعقد إلى الأشكال المسطحة التي تمت مناقشتها سابقًا ، ولكن في العالم الحقيقي ، قد تحتاج إلى تقسيم الشكل المسطح إلى الكثير من الأشكال المسطحة للحصول على نتيجة حسابية دقيقة.
طريقة جيدة للبدء هي البحث عن الخطوط الموازية أو التي تشكل زاوية معينة ، لأن معظم الأشكال المسطحة تتكون من هذه الأشكال
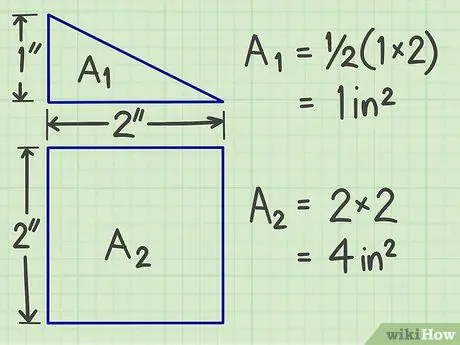
الخطوة 2. احسب المساحة لكل من الأشكال المستوية الناتجة عن الفصل
استخدم الطرق المذكورة أعلاه للحصول على مساحة كل شكل مسطح.
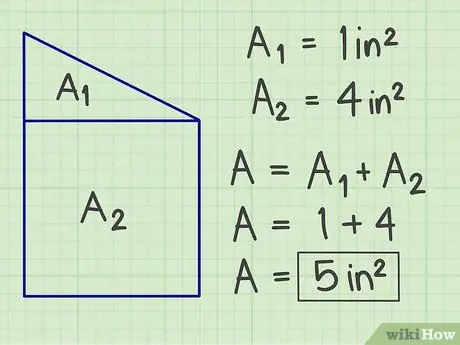
الخطوة 3. اجمع النتائج
اجمع كل المساحات المحسوبة لتحصل على المساحة الكلية لشكل المستوى المعقد.
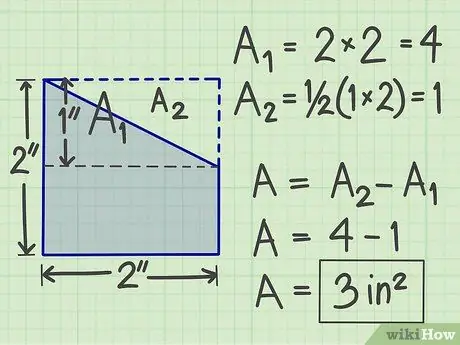
الخطوة 4. استخدم طريقة أخرى
هناك العديد من الطرق الأخرى التي يمكنك تجربتها ، اعتمادًا على شكل الشكل المسطح المعقد. على سبيل المثال ، يمكنك أيضًا إضافة شكل مستوى وهمي إليه بحيث يصبح شكل مستوى هندسي قياسي. بعد ذلك احسب المساحة ، ثم اطرح مساحة الشكل المسطح التخيلي الذي استخدمته لإضافته.
نصائح
- استخدم هذه الآلة الحاسبة إذا كنت بحاجة إلى مساعدة في حل العمليات الحسابية.
- اطلب المساعدة من صديق إذا كنت لا تزال تواجه مشكلة!
تحذير
- من الأفضل دائمًا التحقق مرة أخرى من نتائج الحساب للتأكد من صحتها!
- تأكد من أن الوحدات التي تستخدمها كلها متشابهة (سم ، م ، بوصة ، إلخ) عند الحساب ، حتى لا تتعرض لسوء التقدير بسبب الوحدات المختلطة!






