3 طرق لحساب معامل ارتباط رتبة سبيرمان

2024 مؤلف: Jason Gerald | [email protected]. آخر تعديل: 2023-12-16 10:53

باستخدام معامل ارتباط رتبة سبيرمان ، يمكننا تحديد ما إذا كان هناك متغيرين لهما علاقة دالة رتيبة (أي عندما يزيد رقم واحد ، سيزداد الرقم الآخر أيضًا ، أو العكس). لحساب معامل ارتباط رتبة سبيرمان ، تحتاج إلى ترتيب مجموعات البيانات ومقارنتها للعثور على د²، ثم أدخل البيانات في صيغة معامل ارتباط رتبة سبيرمان القياسية أو المبسطة. يمكنك أيضًا حساب هذه المعاملات باستخدام صيغ Excel أو الأمر R.

خطوة

طريقة 1 من 3: طريقة يدوية

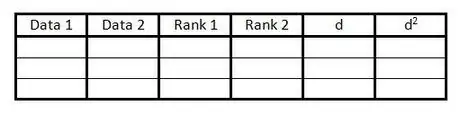
الخطوة 1. قم بإنشاء جدول

يستخدم الجدول لتضمين جميع المعلومات اللازمة لحساب معامل ارتباط رتبة سبيرمان. أنت بحاجة إلى طاولة مثل هذا:

• قم بإنشاء 6 أعمدة بالعناوين ، كما في المثال.
• قم بإعداد العديد من الصفوف الفارغة مثل عدد أزواج البيانات.

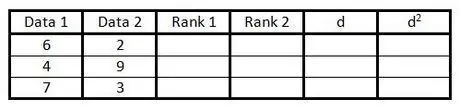
الخطوة 2. املأ أول عمودين بأزواج البيانات

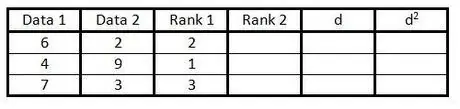
الخطوة 3. أدخل ترتيب العمود الأول لمجموعات البيانات في العمود الثالث من 1 إلى n (عدد البيانات)

قم بتقييم 1 لأدنى قيمة ، وتصنيف 2 لأدنى قيمة تالية ، وهكذا.

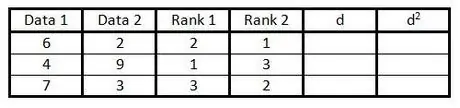
الخطوة 4. في العمود الرابع ، افعل الشيء نفسه كما في الخطوة 3 ، ولكن لترتيب البيانات في العمود الثاني

• 

  إذا كانت هناك بيانات (أو أكثر) لها نفس القيمة ، فاحسب متوسط تصنيف البيانات ، ثم أدخلها في جدول بناءً على قيمة المتوسط هذه.

  في المثال الموجود على اليمين ، توجد قيمتان للرقم 5 في التصنيفين 2 و 3. نظرًا لوجود 5s ، ابحث عن متوسط التصنيفات. متوسط 2 و 3 هو 2.5 ، لذا أدخل قيمة تصنيف 2.5 لكلا القيمتين 5.

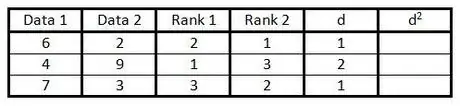
الخطوة 5. في العمود "d" احسب الفرق بين الرقمين الموجودين في عمود الترتيب

أي إذا كان أحد الأعمدة في المرتبة 1 والعمود الآخر في المرتبة 3 ، يكون الفرق هو 2. (لا تهم العلامة ، لأن الخطوة التالية هي تربيع القيمة.)

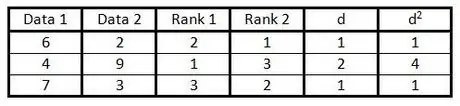
الخطوة 6. قم بتربيع كل رقم في العمود "d" واكتب النتيجة في العمود "d²".

الخطوة 7. اجمع كل البيانات في العمود d²".

والنتيجة د².

الخطوة 8. اختر إحدى الصيغ التالية:

• إذا لم يكن أي من التصنيفات هو نفسه كما في الخطوة السابقة ، أدخل هذه القيمة في صيغة معامل ارتباط رتبة سبيرمان المبسطة

  

  واستبدل "n" بعدد أزواج البيانات للحصول على النتيجة.

  

• إذا كان هناك تصنيف مشابه في الخطوة السابقة ، فاستخدم معادلة معامل ارتباط رتبة سبيرمان القياسية:

  

الخطوة 9. تفسير النتائج

يمكن أن تختلف القيمة بين -1 و 1.

• إذا كانت القيمة قريبة من -1 ، يكون الارتباط سالبًا.
• إذا كانت القيمة قريبة من 0 ، فلا يوجد ارتباط خطي.
• إذا كانت القيمة قريبة من 1 ، يكون الارتباط موجبًا.

الطريقة 2 من 3: استخدام Excel

الخطوة 1. قم بإنشاء عمود جديد للبيانات مع ترتيبها

على سبيل المثال ، إذا كانت بياناتك في العمود A2: A11 ، فاستخدم الصيغة "= RANK (A2، A $ 2: A $ 11)" وانسخها حتى تغطي جميع الأعمدة والصفوف.

الخطوة 2. قم بتغيير نفس التصنيف كما هو موضح في الخطوتين 3 و 4 من الطريقة 1

الخطوة 3. في الخلية الجديدة ، احسب الارتباط بين عمودي الترتيب بالصيغة "= CORREL (C2: C11، D2: D11)"

في هذا المثال ، تشير C و D إلى العمود الذي يوجد به الترتيب. سيتم ملء الخلية الجديدة بترتيب Spearman Rank Correlation.

طريقة 3 من 3: استخدام R

الخطوة الأولى. قم بتثبيت برنامج R أولاً إذا لم يكن لديك بالفعل

(انظر

الخطوة الثانية: احفظ بياناتك بصيغة CSV ، ضع البيانات التي تريد العثور على الارتباط في أول عمودين

يمكننا القيام بذلك عن طريق استخدام قائمة "حفظ باسم".

الخطوة 3. افتح محرر R

إذا كنت تعمل من المحطة ، فما عليك سوى تشغيل R. إذا كنت تعمل من سطح المكتب ، فانقر فوق الرمز R.

الخطوة 4. اكتب الأمر التالي:

• د <- read.csv ("NAME_OF_YOUR_CSV.csv") واضغط على Enter.
• cast (رتبة (d [، 1])، رتبة (d [، 2]))

نصائح

يجب أن تتكون البيانات من 5 أزواج على الأقل حتى يمكن رؤية الاتجاه (عدد البيانات هو 3 أزواج في المثال فقط لتبسيط العمليات الحسابية.)

تحذير

• يحدد معامل ارتباط رتبة سبيرمان قوة الارتباط فقط حيث ترتفع البيانات أو تنخفض باستمرار. إذا كان هناك اتجاه آخر في البيانات ، فهو ارتباط رتبة سبيرمان لا سيوفر تمثيلًا دقيقًا.
• تعتمد هذه الصيغة على افتراض عدم وجود تصنيفات متساوية. عندما يكون هناك نفس الرتبة كما في المثال ، يجب أن نستخدم هذا التعريف: معامل الارتباط لحظة الضرب بالرتبة.