- مؤلف Jason Gerald gerald@how-what-advice.com.
- Public 2023-12-16 10:53.
- آخر تعديل 2025-01-23 12:06.
الرياضيات صعبة. من السهل أن تنسى حتى المفاهيم الأساسية عندما تحاول تذكر العديد من المبادئ والأساليب المختلفة. فيما يلي طريقتان جديدتان لتبسيط الكسور.
خطوة
طريقة 1 من 4: استخدام العامل المشترك الأكبر

الخطوة 1. اكتب عوامل البسط والمقام
العوامل هي الأرقام التي يمكنك ضربها للحصول على رقم آخر. على سبيل المثال ، 3 و 4 عاملان للعدد 12 لأنه يمكنك ضربهما معًا للحصول على 12. لكتابة عوامل الرقم ، ما عليك سوى كتابة جميع الأرقام التي يمكن ضربها للحصول على هذا الرقم ، وقابلة للقسمة. بالعوامل.
-
اكتب عوامل العدد من الأصغر إلى الأكبر ، دون أن تنسى تضمين العامل 1. على سبيل المثال ، إليك كيفية كتابة بسط ومقام الكسر 24/32:
- 24: 1, 2, 3, 4, 6, 8, 12, 24.
- 32: 1, 2, 4, 8, 16, 32.

الخطوة الثانية: أوجد العامل المشترك الأكبر (GCF) للبسط والمقام
العامل المشترك الأكبر هو أكبر رقم يمكنه قسمة رقمين أو أكثر بالتساوي. بعد أن تقوم بتدوين جميع عوامل العدد ، كل ما عليك فعله هو إيجاد أكبر رقم متماثل في كلا قائمتَي العوامل.
-
24: 1, 2, 3, 4, 6,
الخطوة 8., 12, 24.
-
32: 1, 2, 4,
الخطوة 8., 16, 32.
-
العامل المشترك الأكبر للعددين 24 و 32 هو 8 لأن 8 هو أكبر عدد يمكن أن يقسم 24 و 32 بالتساوي.

اختزل الكسور الخطوة 3 الخطوة 3. اقسم البسط والكسر على العامل المشترك الأكبر
الآن بعد أن حصلت على العامل المشترك الأكبر ، كل ما عليك فعله هو قسمة البسط والمقام على هذا الرقم لتبسيط الكسر إلى أبسط صورة. هيريس كيفية القيام بذلك:
- 24/8 = 3
- 32/8 = 4
- الكسر البسيط هو 3/4.

اختزل الكسور الخطوة 4 الخطوة 4. تحقق من عملك
إذا كنت تريد التأكد من تبسيط الكسر بشكل صحيح ، فما عليك سوى ضرب البسط والمقام الجديدين في العامل المشترك الأكبر لاستعادة الكسر الأصلي. هيريس كيفية القيام بذلك:
- 3 * 8 = 24
- 4 * 8 = 32
-
لقد عدت إلى شكلها الأصلي ، وهو 24/32.
يمكنك أيضًا فحص الكسر للتأكد من أنه لا يمكن تبسيطه أكثر. بما أن 3 عدد أولي ، فلا يمكن قسمة هذا العدد إلا على 1 وعلى نفسه ، وأربعة لا يقبل القسمة على 3 ، لذلك لا يمكن تبسيط الكسر أكثر من ذلك
الطريقة 2 من 4: حافظ على القسمة على الأعداد الصغيرة

اختزل الكسور الخطوة 5 الخطوة 1. اختر رقمًا صغيرًا
باستخدام هذه الطريقة ، ما عليك سوى اختيار رقم صغير ، مثل 2 أو 3 أو 4 أو 5 أو 7 لتبدأ به. انظر إلى الكسور لتتأكد من أن كل جزء قابل للقسمة على الرقم الذي اخترته. على سبيل المثال ، إذا كان لديك كسر 24/108 ، فلا تختار 5 لأنها غير قابلة للقسمة على 5. ومع ذلك ، إذا كان لديك كسر 25/60 ، فإن 5 هو الرقم الصحيح لاستخدامه.
بالنسبة للكسر 24/32 ، 2 عدد جيد. نظرًا لأن كلا الرقمين عدد زوجي ، فإنهما يقبلان القسمة على 2

اختزل الكسور الخطوة 6 الخطوة الثانية. قسّم بسط الكسر ومقامه على الرقم
سيتكون الكسر الجديد من بسط ومقام جديدين ، والذي تحصل عليه بعد قسمة الجزء العلوي والسفلي من الكسر 24/32 على 2. وإليك كيفية القيام بذلك:
- 24/2 = 12
- 32/2 = 16
- الكسر الجديد هو 12/16.
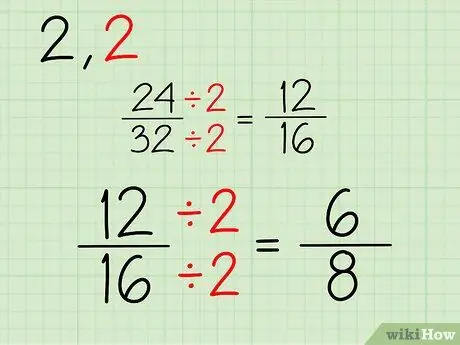
اختزل الكسور الخطوة 7 الخطوة 3. كرر
استمر في هذه العملية. نظرًا لأن كلا العددين عدد زوجي ، يمكنك الاستمرار في القسمة على 2. إذا كان أحد البسط والمقام أو كلاهما عددًا فرديًا ، فيمكنك محاولة القسمة على رقم آخر. إليك عملية تبسيط كسر 12/16:
- 12/2 = 6
- 16/2 = 8
- الكسر الجديد هو 6/8.

اختزل الكسور الخطوة 8 الخطوة 4. استمر في قسمة الرقم حتى يصبح غير قابل للقسمة
البسط والمقام الجديدين عبارة عن أعداد زوجية أيضًا ، لذا يمكنك الاستمرار في القسمة على 2. وإليك كيفية القيام بذلك:
- 6/2 = 3
- 8/2 = 4
- الكسر الجديد هو 3/4.

اختزل الكسور الخطوة 9 الخطوة 5. تأكد من أن الكسر لا يمكن تبسيطه أكثر من ذلك
في الكسر 3/4 ، 3 عدد أولي ، وبالتالي فإن العوامل هي 1 ونفسه فقط ، و 4 لا يقبل القسمة على 3 ، لذلك لا يمكن تبسيط الكسر أكثر من ذلك. إذا لم يعد من الممكن تقسيم بسط الكسر أو مقامه على الرقم الذي حددته ، فقد لا يزال بإمكانك تقسيمه على رقم آخر.
على سبيل المثال ، إذا كان لديك الكسر 10/40 ، وقسمت البسط والمقام على 5 ، تكون النتيجة 2/8. لا يمكنك الاستمرار في قسمة البسط والكسر على 5 ، لكن يمكنك قسمة كلاهما على 2 بحيث تكون النتيجة النهائية 1/4

اختزل الكسور الخطوة 10 الخطوة 6. تحقق من عملك
اضرب 3/4 في 2/2 ثلاث مرات لتتأكد من حصولك على الكسر الأولي ، وهو 24/32. هيريس كيفية القيام بذلك:
- 3/4 * 2/2 = 6/8
- 6/8 * 2/2 = 12/16
- 12/16 * 2/2 = 24/32.
- لاحظ أنك تقسم 24/32 على 2 * 2 * 2 ، وهو ما يماثل القسمة على 8 ، وهو أكبر معامل إجمالي للقيمتين 24 و 32.
طريقة 3 من 4: كتابة العوامل

اختزل الكسور الخطوة 11 الخطوة 1. اكتب الكسر
اترك مساحة كبيرة على الجانب الأيمن من ورقتك - ستحتاج إليها لتدوين العوامل.

اختزل الكسور الخطوة 12 الخطوة الثانية: اكتب عوامل البسط والمقام
وحدها عوامل الاثنين. أسهل طريقة هي كتابة العوامل فوق بعضها البعض. ابدأ بالرقم 1 واكتب العوامل.
-
على سبيل المثال ، إذا كان الكسر 24/60 ، فابدأ بالرقم 24.
اكتب: ٢٤ - ١ ، ٢ ، ٣ ، ٤ ، ٦ ، ٨ ، ١٢ ، ٢٤
-
ثم الرقم 60.
اكتب: 60-1 ، 2 ، 3 ، 4 ، 5 ، 6 ، 10 ، 12 ، 15 ، 20 ، 30 ، 60

اختزل الكسور الخطوة 13 الخطوة الثالثة. ابحث وقسم على العامل المشترك الأكبر
يمكن كتابة هذا المصطلح كـ GCF في كتابك المطبوع. ما هو أكبر عدد يمكن أن يقسم البسط والمقام؟ مهما كان الرقم ، اقسم كلا الرقمين على هذا الرقم.
على سبيل المثال ، أكبر رقم يمثل عاملًا لكلا العددين هو 12. وهكذا ، نقسم 24 على 12 و 60 على 12 ، مما يعطينا 2/5 - الكسر البسيط
طريقة 4 من 4: استخدام شجرة العامل الأساسي

اختزل الكسور الخطوة 14 الخطوة 1. أوجد العوامل الأولية للبسط والمقام
الرقم الأولي هو رقم لا يمكن تقسيمه على أي رقم آخر (بخلاف نفسه و 1 بالطبع). 2 و 3 و 5 و 7 و 11 هي أمثلة على الأعداد الأولية.
- ابدأ بالبسط. من 24 ، اقسم إلى 2 و 12. نظرًا لأن 2 عدد أولي بالفعل ، فلن تحتاج إلى تقسيمه بعد الآن! ثم قسّم 12 إلى رقمين: 2 و 6. 2 أعداد أولية - عظيم! قسّم الآن 6 إلى رقمين: 2 و 3. لديك الآن 2 و 2 و 2 و 3 كأعداد أولية.
- الآن اعمل على المقام. من 60 ، قسّم شجرتك إلى 2 و 30. 30 ثم اقسم إلى 2 و 15. ثم قسّم 15 إلى 3 و 5 ، وكلاهما عدد أولي. الآن لديك 2 و 2 و 3 و 5 كأعداد أولية.
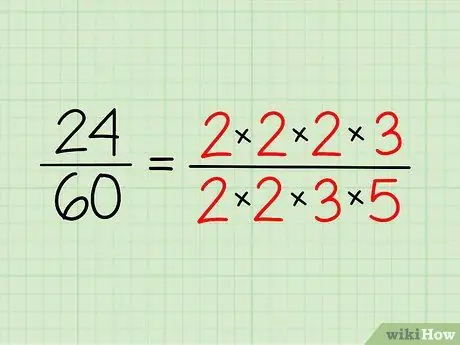
اختزل الكسور الخطوة 15 الخطوة 2. اكتب التحليل الأولي لكل رقم
اكتب الأعداد الأولية التي لديك لكل عدد واكتبها بصيغة الضرب. لست مضطرًا لمضاعفتها - إنها مجرد طريقة لتسهيل الرؤية.
- إذن ، بالنسبة إلى 24 ، لديك 2 × 2 × 2 × 3 = 24.
- بالنسبة لـ 60 ، لديك 2 × 2 × 3 × 5 = 60

اختزل الكسور الخطوة 16 الخطوة 3. تخلص من نفس العوامل
يمكن تجاهل أي رقم يمثل جزءًا من كلا الرقمين. في هذا المثال ، العوامل المتساوية هي زوج من 2s وواحدة 3. وداعا!
- الباقي 2 و 5 - أو 2/5! نفس الإجابة التي حصلنا عليها بالطريقة أعلاه.
- إذا كان بسط الكسر ومقامه أعدادًا زوجية ، فلا تقسم على اثنين فقط. استمر في إجراء القسمة حتى لا يمكن تقسيم الرقم الذي تحصل عليه مرة أخرى.






