- مؤلف Jason Gerald gerald@how-what-advice.com.
- Public 2024-01-15 08:08.
- آخر تعديل 2025-01-23 12:06.
تعد إضافة الكسور وطرحها مهارة مهمة يجب امتلاكها. تظهر الكسور في الحياة اليومية طوال الوقت ، خاصة في فصول الرياضيات ، من الابتدائية إلى الكلية. اتبع هذه الخطوات لتتعلم كيفية جمع وطرح الكسور ، من الكسور المتكافئة ، أو الكسور غير المتساوية ، أو الأعداد الكسرية ، أو الكسور الشائعة. إذا كنت تعرف طريقة ما بالفعل ، فمن السهل حقًا حل الكسور الأخرى!
خطوة
طريقة 1 من 4: جمع وطرح الكسور ذات المقام نفسه
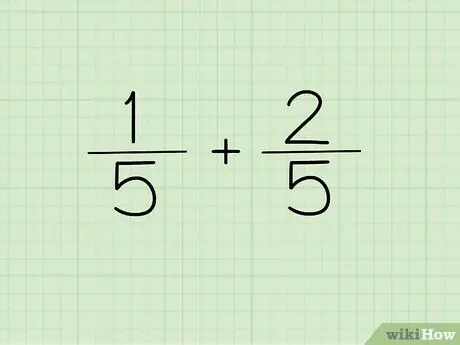
الخطوة الأولى. اكتب سؤالك
إذا كان مقام الكسرين اللذين تريد إضافتهما أو طرحهما هو نفسه ، فاكتب المقام مرة واحدة كمقام إجابتك.
بمعنى آخر ، لا يلزم كتابة 1/5 و 2/5 كـ 1/5 + 2/5 =؟ ولكن يمكن كتابتها كـ (1 + 2) / 5 =؟. المقامات هي نفسها ، لذا لا يمكن كتابتها إلا مرة واحدة. يتم الجمع بين البسطين
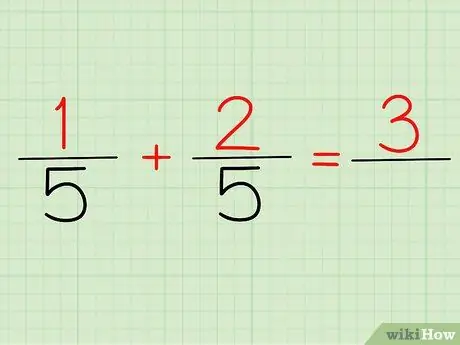
الخطوة 2. اجمع البسط
البسط هو الرقم الموجود فوق أي كسر. إذا نظرنا إلى المسألة أعلاه ، فإن 1/5 و 2/5 ، 1 و 2 هي البسط.
سواء كتبتها 1/5 + 2/5 أو (1 + 2) / 5 ، ستكون إجابتك هي نفسها: 3! لأن 1 + 2 = 3

الخطوة 3. اترك المقام
بما أن المقامات متشابهة ، فلا تفعل شيئًا مع القواسم! لا تضيف أو تطرح أو تضرب أو تقسم. فليكن.
إذن ، من نفس المثال ، المقام هو 5. صحيح! 5 هو العدد السفلي من الكسر. لدينا نصف الجواب

الخطوة 4. اكتب إجابتك
الآن ، كل ما عليك فعله هو كتابة البسط والمقام! إذا استخدمت المثال أعلاه ، فستكون إجابتك 3/5.
ما هو البسط؟ 3. المقام الخاص بك؟ 5. إذن ، 1/5 + 2/5 أو (1 + 2) / 5 يساوي 3/5.
طريقة 2 من 4: جمع وطرح الكسور ذات المقامات المختلفة

الخطوة الأولى. أوجد المقام المشترك الأصغر
أي أن أصغر المقام هو نفسه لكلا الكسرين. افترض أن لدينا الكسرين 2/3 و 3/4. ما هو المقام؟ 3 و 4. لإيجاد المقام المشترك الأصغر لكلا الكسرين ، يمكنك القيام بذلك بثلاث طرق:
- اكتب مضاعفات. مضاعفات 3 هي 3 ، 6 ، 9 ، 12 ، 15 ، 18 … وهكذا. مضاعفات 4؟ 4 ، 8 ، 12 ، 16 ، 20 ، وهكذا. ما هو أصغر عدد يكون من مضاعفات الاثنين؟ 12! هذا هو القاسم المشترك الأصغر.
-
التحليل الأولي. إذا كنت تعرف العوامل ، يمكنك إجراء التحليل الأولي. أي أنك تبحث عن الأرقام التي يتكون منها المقام. بالنسبة للرقم 3 ، العاملان هما 3 و 1. بالنسبة للرقم 4 ، العاملان هما 2 و 2. ثم ، أنتم جميعًا. 3 x 2 x 2 = 12. المقام المشترك الأصغر!
اضرب كل الأعداد في العدد الأصغر. في بعض المسائل ، مثل هذه ، يمكنك ضرب كلا العددين - 3 × 4 = 12. ومع ذلك ، إذا كان لديك مقام كبير ، فلا تفعل هذا! لا تريد أن تضرب 56 × 44 وتخرج كل شيء لتحصل على 2،464

الخطوة 2. اضرب المقام في العدد المطلوب للحصول على أصغر مقام مشترك
بعبارة أخرى ، تريد أن تكون جميع المقامات متساوية. في مثالنا ، نريد أن يكون المقام هو 12. لتغيير 3 إلى 12 ، تضرب 3 في 4. لتغيير 4 إلى 12 ، تضرب 4 في 3. سيكون نفس المقام هو مقام إجابتك النهائية.
-
إذن 2/3 يصبح 2/3 × 4 و 3/4 يصبح 3/4 × 3. أي ، لدينا الآن 2/12 و 3/12. لكننا لم ننتهي بعد!
- ستلاحظ أنه يتم ضرب القواسم ببعضها البعض. يمكن القيام بذلك في هذه الحالة ، ولكن ليس في جميع المواقف. في بعض الأحيان ، بدلاً من ضرب كلا المقامين ، يمكنك ضرب كلا المقام في رقم آخر للحصول على الرقم الأصغر.
- ثم في مسائل أخرى ، تحتاج أحيانًا إلى ضرب مقام واحد لجعله يساوي مقام الكسر الآخر في المسألة.

الخطوة 3. اضرب البسط بنفس الرقم
عندما تضرب المقام في رقم ، يجب أيضًا أن تضرب البسط في نفس الرقم. ما فعلناه في الخطوة الأخيرة ليس سوى جزء من عملية الضرب التي يجب القيام بها.
لدينا 2 / 3x4 و 2 / 4x3 كخطوة أولى - ثم في الخطوة الثانية ، 2 × 4/3 × 4 و 3 × 3/4 × 3. أي أن أرقامنا الجديدة هي 8/12 و 9 / 12. ممتاز
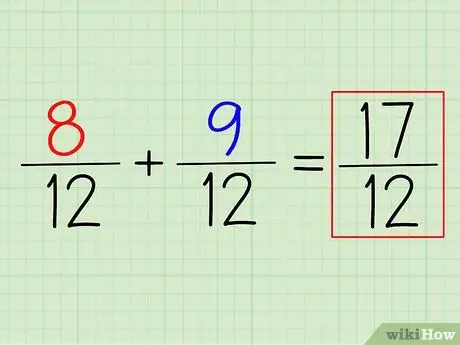
الخطوة 4. اجمع (أو اطرح) البسط للحصول على الإجابة
لإضافة 8/12 + 9/12 ، كل ما عليك فعله هو جمع البسط. تذكر: اترك المقام. أصغر قاسم مشترك تجده هو المقام النهائي.
في هذا المثال (8 + 9) / 12 = 17/12. لتحويله إلى عدد كسري ، ما عليك سوى طرح المقام من البسط وكتابة الباقي. في هذه الحالة ، 17/12 = 1 5/12
طريقة 3 من 4: جمع وطرح الكسور المختلطة والمشتركة
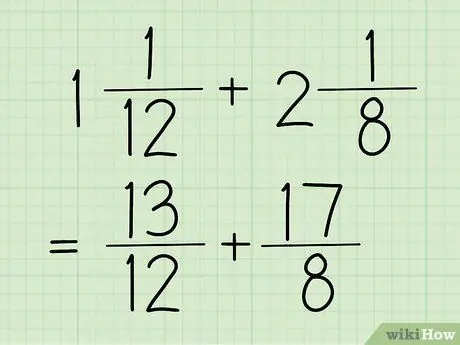
الخطوة 1. حوّل الكسور المختلطة إلى كسور مشتركة
الرقم الكسري هو كسر به عدد صحيح وكسر ، كما في المثال أعلاه (1 5/12). في الوقت نفسه ، الكسر العادي هو كسر بسطه (الرقم العلوي) أكبر من المقام (الرقم السفلي). يظهر هذا الكسر أيضًا في الخطوة السابقة ، وهي 17/12.
للأمثلة في هذا القسم ، سنستخدم 13/12 و 17/8

الخطوة 2. أوجد القاسم المشترك
هل تتذكر الطرق الثلاث لإيجاد المقام المشترك الأصغر؟ بكتابة المضاعفات أو استخدام العوامل الأولية أو ضرب القواسم.
لنجد مضاعفات المثال ، 12 و 8. ما هو أصغر عدد مشترك بينهما؟ 24. 8 و 16 و 24 و 12 و 24 - بنغو

الخطوة الثالثة. اضرب البسط والمقام لإيجاد الكسر المكافئ
يجب تغيير كلا المقامين إلى 24. كيف تقوم بتحويل 12 إلى 24؟ اضرب ب 2. 8 إلى 24؟ اضرب بثلاثة. لكن لا تنسى - عليك أن تضرب البسط أيضًا!
إذن (13 × 2) / (12 × 2) = 26/24. و (17 × 3) / (8 × 3) = 51/24. نحن على وشك الانتهاء من هذا

الخطوة 4. اجمع أو اطرح الكسور
الآن بعد أن أصبح لديك نفس المقام ، يمكنك بسهولة جمع البسطين معًا. تذكر فقط اترك المقام!
26/24 + 51/24 = 77/24. هذا هو مجموعك! ومع ذلك ، كانت الأرقام في الأعلى كبيرة جدًا …

الخطوة 5. تحويل إجابتك مرة أخرى إلى أرقام مختلطة
يبدو العدد الكبير جدًا الموجود أعلى الكسر غريبًا بعض الشيء - لا يمكنك تحديد حجم الكسر. كل ما عليك فعله هو طرح المقام من البسط بشكل متكرر حتى يتعذر طرحه مرة أخرى وكتابة الباقي.
-
في هذا المثال ، 77 ناقص 24 في 3 مرات. أي 24 × 3 = 72. والباقي هو 5! إذن ما هي نتيجتك النهائية؟ 3 5/24.
بكل صدق!
طريقة 4 من 4: جمع وطرح الكسور بدون إيجاد المضاعف المشترك الأصغر
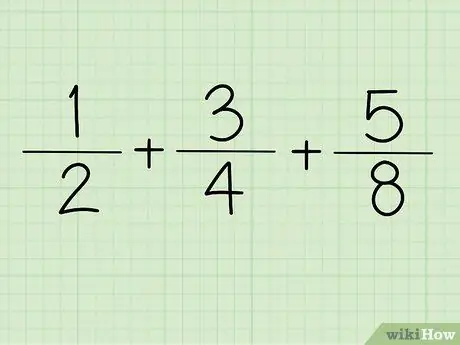
الخطوة 1. اكتب الكسر
على سبيل المثال + +

الخطوة الثانية. قم بحل البسط أولاً
- اضرب في بسط الكسر الآخر.
- اضرب 1 ب 4 ب 8. [32]
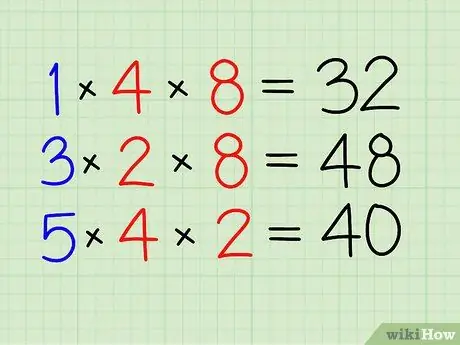
الخطوة 3. افعل الشيء نفسه مع الكسور الأخرى
- اضرب 3 ب 2 ب 8. [48]
- أخيرًا ، اضرب 5 في 4 في 2. [40]
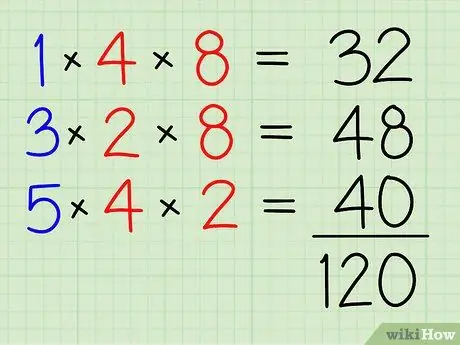
الخطوة 4. اجمعهم جميعًا معًا
32+48+40=120
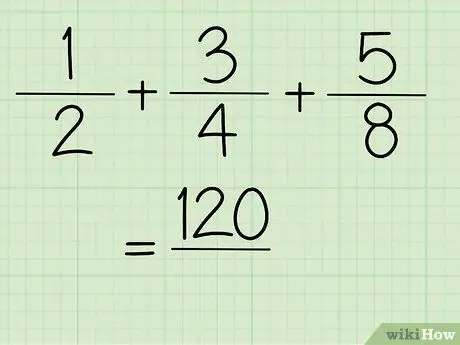
الخطوة 5. الآن ، تحصل على قيمة البسط

الخطوة 6. حل مقام الكسر

الخطوة 7. اضرب كل مقامات الكسور
2×4×8=64

الخطوة 8. الآن تحصل على النتيجة
120/64 = 1 56/64 = 1 ⅞
تحذير
- تسمح لك هذه الطريقة بضرب الأعداد الكبيرة.
- قد تحتاج إلى آلة حاسبة لحساب هذه الطريقة.






