- مؤلف Jason Gerald gerald@how-what-advice.com.
- Public 2024-01-15 08:08.
- آخر تعديل 2025-01-23 12:06.
هناك طرق مختلفة للقيام بالقسمة. يمكنك قسمة الكسور العشرية أو الكسور أو حتى الأس ، واستخدام القسمة الطويلة أو القصيرة. إذا كنت تريد معرفة الطرق المختلفة لقسمة الأرقام ، فاتبع الخطوات أدناه.
خطوة
طريقة 1 من 5: أداء قسم السلسلة الطويلة

الخطوة 1. اكتب الأسئلة
للقيام بالقسمة المطولة ، ضع المقام (الرقم الذي سيقسمه) خارج شريط المقسوم عليه ، والبسط (الرقم المراد تقسيمه) داخل شريط المقسوم عليه.
على سبيل المثال: 136 3

الخطوة 2. قسّم الرقم الأول من البسط على المقام (إن أمكن)
في هذا المثال ، 1 غير قابل للقسمة على 3 ، لذا ضع 0 فوق شريط المقسوم عليه وانتقل إلى الخطوة التالية. اطرح 1 في 0 وضع النتيجة تحت الرقم 1.

الخطوة الثالثة. قسّم رقم باقي الرقم الأول من البسط والرقم الثاني من البسط على المقام
نظرًا لأنه لا يمكن قسمة 1 على 3 ، فلا يزال الرقم 1 مستخدمًا. تحتاج إلى طرح 3. الآن ، قسّم 13 على 3. بما أن 3 × 4 = 12 ، ضع 4 فوق شريط المقسوم عليه (على يمين 0) ، ثم اطرح 13 على 12 واكتب النتيجة أدناه.

الخطوة 4. قسّم الأرقام المتبقية على المقام
اخفض الرقم 6 على يمين 1 ، لتحصل على 16. الآن ، قسّم 16 على 3. بما أن 3 × 5 = 15 ، اكتب الرقم 5 على يمين الرقم 4 ، واطرح 16 على 15 واكتب النتيجة (16-15 = 1) تحتها.

الخطوة 5. اكتب الباقي بجانب حاصل القسمة
إجابتك النهائية هي 45 مع بقاء 1 ، أو 45 R1.
الطريقة 2 من 5: أداء التقسيمات القصيرة

الخطوة 1. اكتب الأسئلة
اكتب المقام (الرقم المراد تقسيمه) خارج شريط المقسوم عليه ، والبسط (الرقم المراد تقسيمه) داخل شريط المقسوم عليه. لاحظ أنه في القسمة المختصرة ، لا يمكن أن يكون المقام أكثر من رقم واحد.
على سبيل المثال، 518 4

الخطوة 2. قسّم الرقم الأول من البسط على المقام
5 4 = 1 م 1. ضع حاصل القسمة (1) فوق شريط الفاصل الطويل. اكتب الباقي فوق الرقم الأول من البسط. ضع 1 على 5 لتذكيرك بأن لديك 1 متبقي عند قسمة 5 على 4. يجب أن يبدو 518 الآن كما يلي: 5118

الخطوة الثالثة. قسّم الرقم المكون من الباقي والرقم الثاني من البسط على المقام
الرقم التالي هو 11 الذي يتم الحصول عليه من القيمة المتبقية (1) والرقم الثاني من البسط (1). 11 4 = 2 R 3 لأن 4 × 2 = 8 مع باقي 3. اكتب القيمة المتبقية أعلى الرقم الثاني من البسط. ضع 3 على 1. البسط الأول (518) يبدو الآن كما يلي: 51138

الخطوة 4. قسّم الأرقام المتبقية على المقام
العدد المتبقي هو 38 ؛ الرقم 3 يأتي من باقي المرحلة السابقة ، و 8 هو الرقم الأخير في البسط. احسب 38 4 = 9 R2. بما أن 4 × 9 = 36 ، اكتب "R2" أعلى شريط القسمة لأن 38 - 36 = 2.

الخطوة 5. اكتب الإجابة النهائية
النتيجة النهائية وحاصل القسمة فوق شريط المقسوم عليه. الجواب هو 518 4 = 129 R2.
طريقة 3 من 5: قسمة الكسور

الخطوة 1. اكتب الأسئلة
لقسمة كسر ، اكتب الكسر الأول متبوعًا برمز القسمة ثم الكسر الثاني.
على سبيل المثال: 3/4 5/8

الخطوة 2. اعكس بسط ومقام الكسر الثاني
الكسر الثاني مقلوب الآن.
مثال: 3/4 8/5

الخطوة 3. قم بتغيير رمز القسمة إلى رمز الأوقات
لقسمة كسر ، اضرب الكسر الأول في مقلوب الثاني.
مثال: 3/4 × 8/5
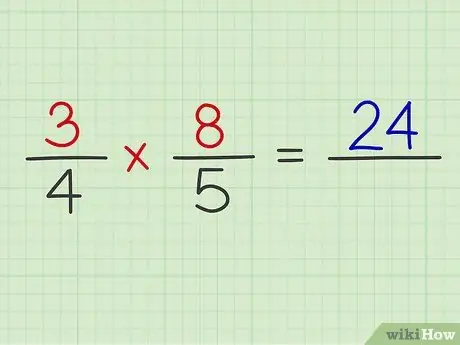
الخطوة 4. اضرب بسط كلا الكسرين
افعل ذلك مثل ضرب كسرين عاديين.
مثال: 3 × 8 = 24
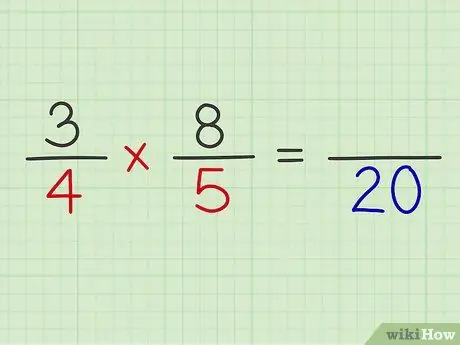
الخطوة 5. اضرب مقامات كلا الكسرين
أكمل العملية الحسابية بضرب الكسرين.
مثال: 4 × 5 = 20
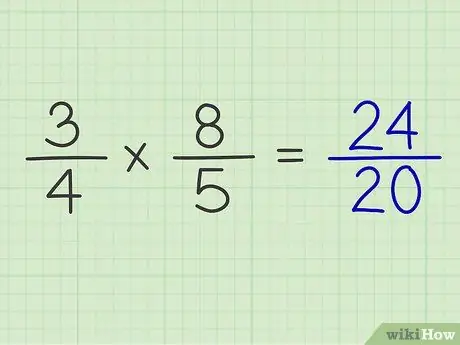
الخطوة 6. ضع حاصل ضرب البسط فوق حاصل ضرب المقام
بعد ضرب البسط والمقام للكسرين ، يمكنك الحصول على نتيجة حساب كلا الكسرين.
مثال: 3/4 × 8/5 = 24/20

الخطوة 7. تبسيط الكسور
لإيجاد العامل المشترك الأكبر ، أو أكبر رقم يقسم البسط والمقام بالتساوي. في هذه الحالة ، العامل المشترك الأكبر بين 24 و 20 هو 4. لإثبات ذلك ، اكتب كل البسط والمقام ، وضع دائرة حول عدد أكبر العوامل المشتركة لكليهما.
- 24: 1, 2, 3, 4, 6, 8, 12, 24
-
20: 1, 2, 4, 5, 10, 20
- بما أن 4 هو العامل المشترك الأكبر بين 24 و 20 ، فما عليك سوى قسمة العددين على 4 لتبسيط الكسر.
- 24/4 = 6
- 20/4 = 5
- 24/20 = 6/5

الخطوة 8. أعد كتابة الكسر في صورة عدد كسري (اختياري)
الحيلة ، ما عليك سوى قسمة البسط على المقام ، وكتابة النتيجة في صورة عدد صحيح. بعد ذلك ، اكتب باقي القسمة كبسط جديد ، ولا يتغير مقام الكسر. بما أن 6 على 5 ينتج عنها 1 مع باقي 1 ، اكتب العدد الصحيح 1 ، متبوعًا بالبسط الجديد 1 ، ثم المقام 5 للحصول على العدد الكسري 1 1/5.
مثال: 6/5 = 1 1/5
طريقة 4 من 5: قسمة الأس

الخطوة الأولى: تأكد من أن الأس / الأسس لهما نفس العدد الأساسي
لا يمكنك قسمة الأسس إلا إذا كان لديهم نفس الرقم الأساسي. خلاف ذلك ، يمكنك محاولة التلاعب بها حتى تحصل على نفس الرقم الأساسي.
مثال: x8 x5

الخطوة 2. اطرح الأس
يمكنك ببساطة طرح الأس الأول بالثاني. لا تمانع في الأرقام الأساسية في الوقت الحالي.
مثال: 8 - 5 = 3
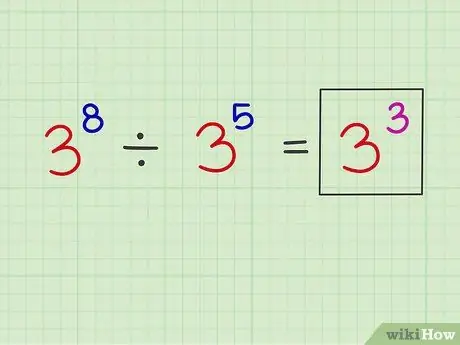
الخطوة 3. ضع الأس الجديد فوق الرقم الأساسي الأصلي
الآن ، يمكنك كتابة الأس الجديد على الرقم الأساسي الأصلي.
مثال: x8 x5 = س3
طريقة 5 من 5: قسمة الأعداد العشرية

الخطوة 1. اكتب الأسئلة
اكتب المقام (الرقم المراد تقسيمه) خارج شريط المقسوم عليه ، والبسط (الرقم المراد تقسيمه) داخل شريط المقسوم عليه. في القسمة العشرية ، هدفك هو تحويل رقم عشري إلى رقم صحيح.
مثال: 65.5.5

الخطوة 2. قم بتغيير المقام إلى عدد صحيح
ما عليك سوى تمرير الفاصلة العشرية برقم واحد إلى اليمين لتغيير 0.5 إلى 5 ، ويعرف أيضًا باسم 5 ، 0.

الخطوة الثالثة. قم بتغيير البسط عن طريق إزاحة الفاصلة العشرية بنفس عدد أرقام المقام
نظرًا لأنك قمت بتحريك الفاصلة العشرية للبسط بمقدار واحد إلى اليمين بحيث تصبح عددًا صحيحًا ، فإن الفاصلة العشرية للمقام تُزاح أيضًا بمقدار رقم واحد إلى اليمين بحيث يتغير 65.5 إلى 655.
إذا قمت بإزاحة الفاصلة العشرية للبسط إلى ما بعد كل أرقامه ، فهذا يعني أنك بحاجة إلى إضافة أصفار إلى الأرقام في كل مرة يتم فيها إزاحة الفاصلة العشرية. على سبيل المثال ، إذا تم إزاحة العلامة العشرية 7 ، 2 بثلاثة أرقام إلى اليمين ، يتغير الرقم إلى 7200 لأن المساحة الفارغة المكونة من رقمين مملوءة بالأصفار

الخطوة 4. ضع العلامة العشرية على شريط القسمة المطول أعلى الفاصلة العشرية في البسط
نظرًا لأنك تقوم بإزاحة الفاصلة العشرية برقم واحد لجعل 0.5 عددًا صحيحًا ، فمن الجيد وضع العلامة العشرية أعلى شريط القسمة بالضبط حيث يتم إزاحة العلامة العشرية ، أي بعد آخر 5 في 655.

الخطوة 5. حل المسألة بقسمة مطولة بسيطة
لقسمة 655 على 5 ، الخطوات هي:
- قسّم رقم المئات في البسط (6) على المقام (5). النتيجة هي 1 مع باقي 1. اكتب الرقم 1 فوق شريط المقسوم عليه ، واكتب 5 تحت الرقم 6 لطرحه.
- يتم طرح باقي 1 من رقم العشرات في البسط (5) بحيث تحصل الآن على 15. اقسم 15 على 5 لتحصل على 3. اكتب 3 فوق شريط المقسوم عليه ، على يمين 1.
- أسقط آخر 5 أرقام. قسّم 5 على 5 لتحصل على 1. اكتب الرقم 1 فوق شريط المقسوم عليه ، على يمين الرقم 3. لا يوجد باقٍ لأن الرقم 5 يقبل القسمة على 5.
- إجابة القسمة المتسلسلة الطويلة هي 655 5 = 131. هذه النتيجة هي نفسها إجابة الأسئلة 65.5 0.5.






