قسمة الكسور على أعداد صحيحة ليس بالأمر الصعب كما يبدو. لقسمة كسر على عدد صحيح ، كل ما عليك فعله هو تحويل العدد الصحيح إلى كسر ، وإيجاد مقلوب الكسر ، وضرب الناتج في الكسر الأول. إذا كنت تريد معرفة كيفية القيام بذلك ، فما عليك سوى اتباع الخطوات التالية:
خطوة
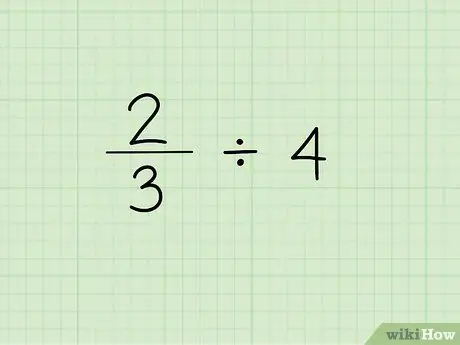
الخطوة الأولى. اكتب المشكلة
الخطوة الأولى لقسمة الكسر على عدد صحيح هي كتابة الكسر متبوعًا بعلامة القسمة والعدد الصحيح الذي تحتاجه لقسمة الكسر. لنفترض أننا نعمل على حل المشكلة التالية: 2/3 4.
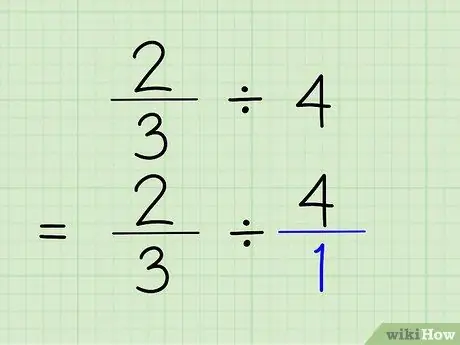
الخطوة 2. تحويل الأعداد الصحيحة إلى كسور
لتحويل عدد صحيح إلى كسر ، كل ما عليك فعله هو وضع العدد الصحيح فوق الرقم 1. يصبح الرقم الصحيح هو البسط ويصبح 1 مقام الكسر. إن قول 4/1 هو في الحقيقة مماثل لقول 4 ، لأنك تظهر فقط أن الرقم يحتوي على "1" 4 مرات. ستكون المشكلة 2/3 4/1.
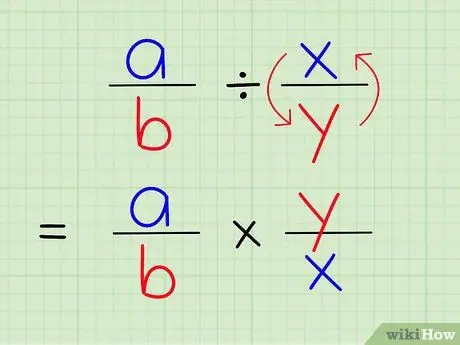
الخطوة 3. قسمة كسر على آخر هو نفس ضرب هذا الكسر في مقلوب كسر آخر
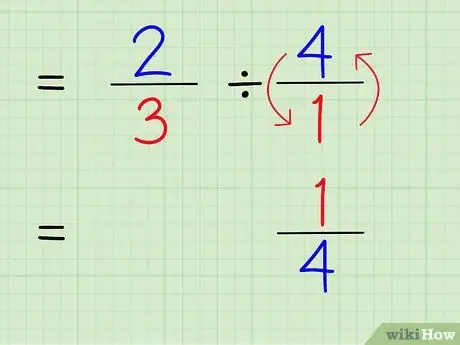
الخطوة 4. اكتب مقلوب العدد الصحيح
لإيجاد مقلوب رقم ، بدّل بسط الرقم ومقامه. لذلك ، للعثور على مقلوب 4/1 ، قم ببساطة بتبديل البسط والمقام حتى يصبح الرقم 1/4.
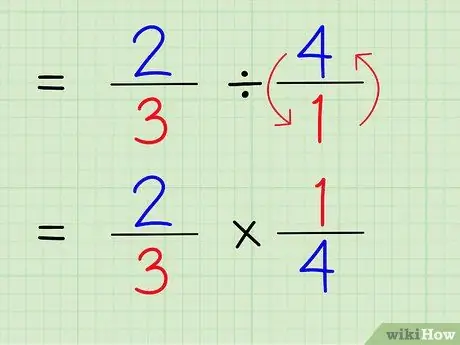
الخطوة 5. قم بتغيير علامة القسمة إلى علامة الضرب
ستكون المشكلة 2/3 × 1/4.
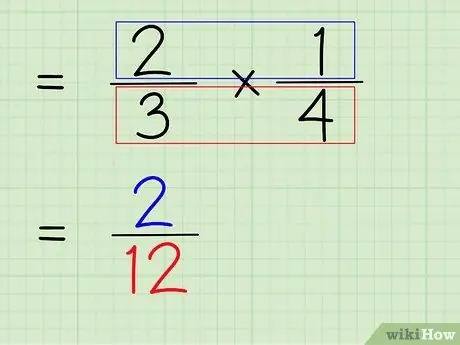
الخطوة 6. اضرب بسط الكسر ومقامه
إذن ، الخطوة التالية هي ضرب بسط الكسر ومقامه للحصول على بسط ومقام جديدين كإجابة نهائية.
- لمضاعفة البسط ، اضرب 2 × 1 لتحصل على 2.
- لمضاعفة المقام ، اضرب 3 × 4 لتحصل على 12.
- 2/3 × 1/4 = 2/12
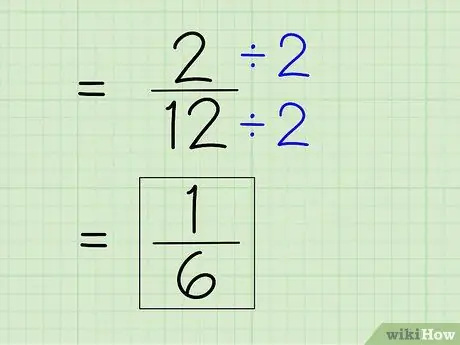
الخطوة 7. بسّط الكسر
لتبسيط كسر ، يجب أن تجد أصغر مقامه ، مما يعني أنه يجب عليك قسمة البسط والمقام على أي رقم يقسم كلا العددين. نظرًا لأن 2 هو البسط ، فسيتعين عليك معرفة ما إذا كان بإمكان 2 قسمة 12 تمامًا - يمكن ذلك لأن 12 عدد زوجي. ثم قسّم البسط والمقام على 2 لتحصل على بسط ومقام جديدين للحصول على إجابة بسيطة.
- 2 ÷ 2 = 1
- 12 ÷ 2 = 6
- يمكن تبسيط الكسر 2/12 ليصبح 1/6. هذه هي إجابتك النهائية.
نصائح
- هذا لمساعدة الذاكرة ، طريقة سهلة لتذكر كيفية القيام بكل هذه الحسابات. ضع هذا في الاعتبار: "من السهل قسمة الكسور وعكس الرقم الثاني والضرب!"
- تباين آخر للطريقة المذكورة أعلاه هو JGB / JBG. لا تغير الرقم الأول. غيّر إلى الضرب. عكس الرقم الأخير. أو B أولاً ثم G.
- إذا ألغيت العملية الحسابية قبل ضربها ، فقد لا تحتاج إلى إيجاد أبسط صورة للكسر لأن النتيجة موجودة بالفعل في أبسط صورة للكسر كما ترى. في مثالنا ، قبل أن نضرب 2/3 × 1/4 ، يمكننا أن نرى أن البسط الأول (2) والمقام الثاني (4) لهما نفس المضاعف 2 ، والذي يمكننا حذفه قبل مواصلة الحساب. هذا يحول المشكلة إلى 1/3 × 1/2 ، مما يعطي نتيجة فورية 1/6 ويوفر لنا الوقت في تبسيط الكسر في مرحلة لاحقة.
- إذا كان أحد الكسور سالبًا ، فإن هذه الطريقة لا تزال قابلة للتطبيق ؛ تأكد من تتبع العلامات أثناء تنفيذ هذه الخطوات.
