إن طرح الكسور من الأعداد الصحيحة ليس بالأمر الصعب كما يبدو. هناك طريقتان رئيسيتان للقيام بذلك: يمكنك تحويل عدد صحيح إلى كسر ، أو يمكنك طرح 1 من العدد الصحيح وتحويل 1 إلى كسر له نفس أساس كسر الطرح. بمجرد أن يكون لديك كسرين لهما نفس الأساس ، يمكنك البدء في الطرح. في كلتا الحالتين ستسمح لك بطرح الكسور من الأعداد الصحيحة بسرعة وسهولة. إذا كنت تريد معرفة كيفية القيام بذلك ، فراجع الخطوة الأولى للبدء.
خطوة
طريقة 1 من 2: تحويل الأعداد الصحيحة إلى كسور
الخطوة الأولى. اكتب المشكلة
لنفترض أنك طرحت الكسر 2/7 من العدد الصحيح 6. كل ما تحتاج إلى معرفته هو أن الجزء العلوي من الكسر يسمى البسط والجزء السفلي من الكسر يسمى المقام. اكتب الأسئلة التالية: 6 - 2/7 =؟
الخطوة 2. تحويل الأعداد الصحيحة إلى كسور
يمكن إعادة كتابة 6 في صورة 6/1 لأن 6/1 تساوي 1 6 مرات ، أو الرقم 6. يمكنك وضع أي عدد صحيح أعلى من 1 ولن تتغير القيمة. هذا يساعد فقط على وضع الأعداد الصحيحة في نفس شكل الكسور. الآن ، ستكون مشكلتك: 6/1 - 2/7 =؟
الخطوة 3. اضرب بسط ومقام العدد الصحيح الأولي في مقام الكسر الأولي ثم اطرح الكسرين
عليك أن تجعل 6/1 و 2/7 لهما نفس الأساس لطرح المصطلحين. للقيام بذلك ، ستحتاج إلى ضرب البسط والمقام 6/1 في 7. هذه طريقة سريعة لإيجاد المضاعف المشترك الأصغر ، أو أصغر مضاعف ، لمقام الكسرين ، 1 و 7. 7 هو الأصغر العدد الذي يقبل القسمة على 1 و 7. كلا الكسرين لهما نفس المقام ، يمكنك طرح بسط الكسر بترك قيمة المقام كما هي ، للحصول على الإجابة النهائية. إليك كيف تفعل ذلك:
-
أولاً ، اضرب 6/1 في 7/7:
6/1 × 7/7 = 42/7
-
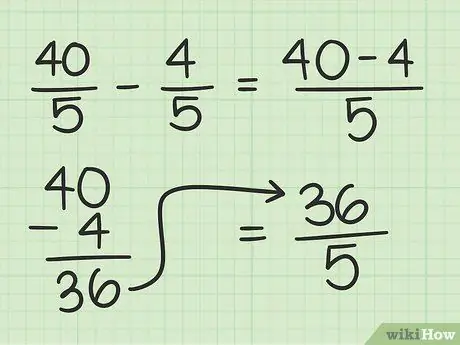
بعد ذلك ، اطرح مقام كلا الكسرين:
42/7 - 2/7 = (42-2)/7 = 40/7
الخطوة 4. اكتب إجابتك النهائية
إذا كنت تريد إجابتك على شكل كسر مشترك (حيث يكون البسط أكبر من المقام) ، تكون بذلك قد انتهيت. إذا كنت تريد أن تكون إجابتك عددًا كسريًا ، حيث تكتب إجابتك النهائية كرقم واحد وكسر واحد ، فكل ما عليك فعله هو قسمة البسط على المقام ، وجعل حاصل القسمة عددًا صحيحًا ، ووضع الباقي على المقام الأول والمقام الذي يبقى كسرًا. هذا ما تفعله:
- أولاً ، قسّم 40 على 7. 40 على 7 يساوي 5 ، مع باقي 5. وذلك لأن 7 × 5 = 35. عندما تطرح 35 من 40 ، يكون لديك طرح 5 ، أو باقي 5.
- بعد ذلك ، اكتب العدد الصحيح: 5.
- خذ الباقي أيضًا 5 وضعه على المقام الأصلي لتحصل على 5/7.
- اكتب العدد الصحيح متبوعًا بالكسر الجديد. تحصل على 5 5/7. وبالتالي ، تتم إعادة كتابة الكسر المشترك 40/7 في صورة عدد كسري 5 5/7.
طريقة 2 من 2: اطرح 1 من العدد الصحيح الأول
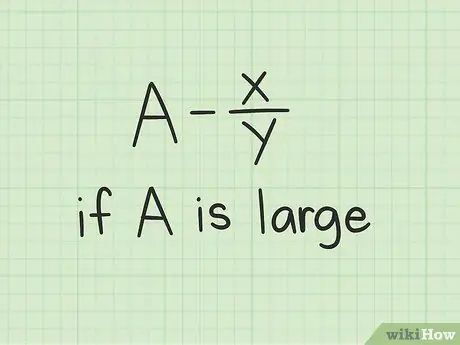
الخطوة الأولى. اكتب المشكلة
سيكون هذا مفيدًا إذا كنت تعلم أنك تريد كتابة إجابتك في صورة عدد مختلط. بهذه الطريقة ، ستسهل عليك الحصول على النتيجة النهائية. دعنا نستخدم نفس المعادلة من الطريقة الأولى ، لمعرفة ما إذا كان يمكنك استخدام أي من الطريقتين في أي موقف. اكتب الأسئلة التالية:
6 - 2/7 = ?
الخطوة 2. اطرح 1 من العدد الصحيح
فقط اطرح 1 من 6 لتحصل على 5. اكتب هذا الرقم.
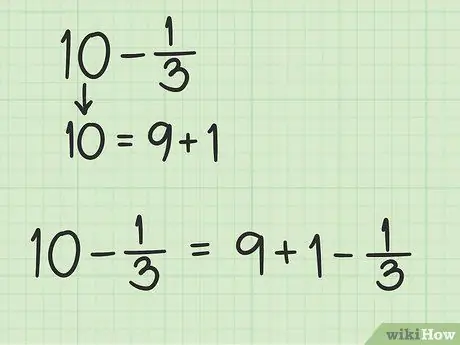
الخطوة الثالثة. حوّل 1 إلى كسر له نفس أساس الكسر
تحتاج إلى تحويل 1 إلى كسر بنفس المقام مثل 7 في 2/7 ، لذا يمكنك طرح 2/7 من الرقم. الآن ، يمكنك تخيل 1 على أنه 1/1 ، ثم ضع في اعتبارك الرقم الذي يتعين عليك ضربه في المقام والبسط 1/1 بحيث يكون مقام الكسور 7 ولكن لهما نفس القيمة. المضاعف المشترك الأصغر ، أو أكبر مضاعف لمقامتي 1 و 7 ، هو 7 ، لأن 7 هو أصغر عدد يقبل القسمة على 1 و 7.
- لذلك ، اضرب 1/1 في 7/7 لتحصل على 7/7.
- لاحظ أن 7/7 لها نفس القيمة مثل 1/1.
الخطوة 4. اكتب مشكلتك الجديدة
الآن ، المشكلة التي لديك هي 5 7/7 - 2/7. هذا يجعل الأرقام أسهل للعمل معها.
الخطوة 5. اطرح الكسر الثاني من الأول
الآن ، فقط اطرح 2/7 من 7/7. عند طرح الكسور ، يجب أن يظل المقام كما هو ، بينما تطرح البسط الثاني من الأول. إذن ، 7/7 - 2/7 = (7-2) / 7 = 5/7.
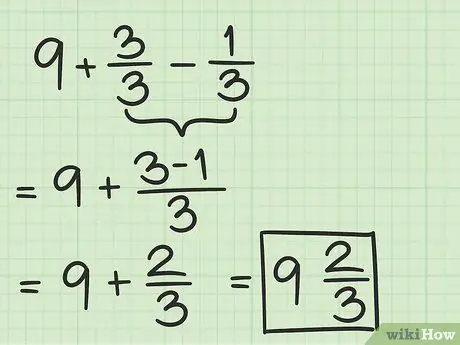
الخطوة 6. اكتب العدد الصحيح بكسره لتحصل على إجابتك النهائية
لقد كتبت بالفعل 5 ، ويمكنك فقط إضافة 2/7 بجانبها. وهكذا ، 6 - 2/7 = 5 5/7. هذه الطريقة أسهل قليلاً إذا كنت تريد إجابتك في شكل عدد مختلط ، لأنك يجب أن تعمل فقط مع الأعداد الصحيحة 1 بدلاً من العدد الصحيح 6 ، ولا يتعين عليك التحويل من الكسور الشائعة إلى الأعداد المختلطة ، كما فعلت في الطريقة الأولى. يمكنك تحديد الطريقة الأنسب لاحتياجاتك.
