3 طرق لحساب السرعة

2024 مؤلف: Jason Gerald | [email protected]. آخر تعديل: 2024-01-16 19:08

السرعة هي حساب لمدى سرعة تحرك شيء ما في وقت واحد. إذا سبق لك أن نظرت إلى عداد السرعة لسيارة متحركة ، فسترى عدد السرعة - كلما تحركت الإبرة أبعد ، زادت سرعة السيارة. هناك عدة طرق لحساب السرعة ، اعتمادًا على نوع المعلومات التي لديك. بشكل عام ، الصيغة السرعة = المسافة / الوقت (أو k = j / w) هي أسهل طريقة لحساب السرعة.

خطوة

الطريقة 1 من 3: استخدام معادلات حساب السرعة القياسية

الخطوة 1. أوجد المسافة التي قطعها جسم ما

الصيغة الأساسية التي يستخدمها معظم الناس للعثور على سرعة شيء ما سهلة الاستخدام للغاية. بادئ ذي بدء ، تحتاج إلى معرفة "مقدار المسافة التي قطعها الجسم المقاس". بمعنى آخر ، ما هي المسافة بين نقطة البداية ونقطة نهاية الكائن؟

هذه الصيغة أسهل للفهم من خلال مثال. لنفترض أننا نسافر بالسيارة إلى ملعب لمسافة "161 كيلومترًا". في بضع خطوات ، يمكننا استخدام هذه المعلومات لإكمال حساب الصيغة

الخطوة 2. أوجد الوقت الذي يستغرقه الجسم لقطع تلك المسافة

المعلومات التالية التي تحتاجها هي المدة التي يستغرقها الكائن للوصول إلى مسافة معينة. بمعنى آخر ، ما هو الوقت الذي يستغرقه الكائن للانتقال من نقطة البداية إلى نقطة النهاية؟

في هذا المثال ، لنفترض أن الكائن يأخذ تقريبًا. ساعتين للوصول إلى الوجهة.

الخطوة 3. اقسم المسافة على الوقت المستغرق لإيجاد سرعة الجسم

ما عليك سوى هاتين القطعتين من المعلومات لمعرفة سرعة الجسم. المسافة إلى الوقت تساوي سرعة الجسم.

في هذا المثال ، 161 كيلومترًا / ساعتان = 80.5 كيلومتر / ساعة.

الخطوة 4. لا تنسى الوحدة المستخدمة

من المهم جدًا استخدام الوحدات الصحيحة في إجابتك (مثل الكيلومترات في الساعة ، إلخ.) بدون هذه الوحدات ، من الصعب جدًا على الأشخاص فهم معنى إجابتك. يمكنك أيضًا أن تخسر نقاطًا إذا استخدمت الوحدة الخطأ عند القيام بمهام من المدرسة.

وحدة السرعة هي وحدة المسافة إلى وحدة الوقت. على سبيل المثال ، نظرًا لأننا نقيس المسافة بالكيلومترات والوقت بالساعات ، فإن الوحدات المستخدمة هي كيلومتر / ساعة (أو كيلومترات في الساعة).

الطريقة 2 من 3: حل الحسابات الأكثر صعوبة

الخطوة الأولى: أوجد عدة متغيرات مختلفة لحل مشكلة المسافة والزمن

بمجرد فهمك للصيغة الأساسية للسرعة ، يمكنك استخدامها لإجراء عمليات حسابية بخلاف السرعة. على سبيل المثال ، إذا كنت تعرف في البداية سرعة الكائن ومتغير آخر فقط ، فيمكنك إعادة ترتيب الصيغة أعلاه للعثور على المعلومات غير المعروفة.

• على سبيل المثال ، لنفترض أننا نعلم أن قطارًا يسافر بسرعة 20 كيلومترًا في الساعة لمدة أربع ساعات ، لكننا لا نعرف المسافة التي قطعها. لمعرفة ذلك ، يمكننا إعادة ترتيب الصيغة بالطريقة التالية:

  السرعة = المسافة / الوقت

  السرعة × الوقت = (المسافة / الوقت) × الوقت

  السرعة × الوقت = المسافة

  20 كم / ساعة × 4 ساعات = المسافة = 80 كيلومترا

الخطوة الثانية. قم بتحويل الوحدات التي تستخدمها حسب الحاجة

في بعض الأحيان ، يمكنك حساب السرعة باستخدام وحدة معينة ، لكنك تحتاج إلى تحويلها إلى وحدة أخرى. في هذه الحالة ، تحتاج إلى استخدام عامل تحويل للحصول على الإجابة وفقًا للوحدات الصحيحة. للقيام بذلك ، اكتب ببساطة العلاقة بين الوحدات في صورة كسر واضربها. عند الضرب ، اعكس الكسر حسب الحاجة لإزالة الوحدات غير المرغوب فيها. هذه الطريقة أسهل بكثير مما تبدو!

• على سبيل المثال ، لنفترض أنه في المثال أعلاه ، نحتاج إلى الإجابة بالأميال بدلاً من الكيلومترات. الميل الواحد يساوي 1.6 كيلومتر. لذلك يمكننا إجراء التحويل على النحو التالي:

  80 كيلومترًا × 1 ميل / 1.6 كيلومتر = 50 ميلا

• تذكر أنه نظرًا لظهور الكيلومترات أسفل الكسر ، فإنها تزيل الكيلومترات من الإجابة السابقة ، وبالتالي تستخدم النتيجة النهائية الأميال.
• يوفر موقع الويب هذا ميزات تحويل لمعظم الوحدات الشائعة الاستخدام.

الخطوة 3. استبدل متغير "المسافة" بصيغة المسافة حسب الحاجة

لا تتحرك الكائنات دائمًا في مسار مستقيم وسلس. إذا كان هذا صحيحًا ، فقد لا تتمكن ببساطة من إدخال قيمة رقمية كوحدة للمسافة في صيغة السرعة القياسية. ومع ذلك ، قد تحتاج إلى استبدال الحرف j في الصيغة k = j / w بصيغة تشبه المسافة التي يقطعها الكائن.

• على سبيل المثال ، لنفترض أن طائرة تدور في الهواء مسافة 20 ميلاً 5 مرات. أكملت الطائرة الجولة في نصف ساعة. في هذا المثال ، ما زلنا بحاجة إلى إيجاد المسافة الإجمالية التي قطعتها الطائرة قبل أن نتمكن من تحديد سرعتها. يمكننا استخدام صيغة حساب المسافة حول دائرة (المسافة حولها) بدلاً من j في هذه الصيغة. هذه الصيغة هي محيط = 2πr حيث r = نصف قطر الدائرة. إليك كيفية حلها:

  ك = (2 × × ص) / ث

  ك = (2 × × 10) /0.5

  ك = 62.83 / 0.5 = 125.66 ميل / ساعة

الخطوة 4. نفهم أن k = j / w يعطي السرعة المتوسطة

الصيغة السهلة والبسيطة التي نستخدمها لإيجاد السرعة لها عيب واحد. القيمة الناتجة تقنيًا هي متوسط السرعة. هذا يعني أن الصيغة تفترض أن الكائن الذي تقيسه يستخدم نفس السرعة أثناء تحركه. كما سنرى أدناه ، فإن إيجاد سرعة جسم في لحظة واحدة سيكون أكثر صعوبة.

لتوضيح هذا الاختلاف ، تخيل آخر مرة سافرت فيها بالسيارة. من غير المحتمل أن تسافر بنفس السرعة التي تسافر بها. ومع ذلك ، ستبدأ رحلتك عادةً بسرعة منخفضة وتزيد سرعتك تدريجيًا على طول الطريق ، وتتوقف بسبب الإشارات الحمراء والاختناقات المرورية وما إلى ذلك. إذا كنت تستخدم معادلة السرعة القياسية لإيجاد السرعة أثناء السفر ، فلا يمكن اكتشاف التغييرات التي طرأت على هذه السرعة. ومع ذلك ، ستحصل على إجابة توضح متوسط السرعة لجميع فروق السرعة التي تسافرها

طريقة 3 من 3: حساب السرعة الفورية

ملحوظة:

يستخدم هذا القسم تقنيات غير مألوفة لدى الأشخاص الذين لم يدرسوا التفاضل والتكامل من قبل. اقرأ مقالاتنا عن حساب التفاضل والتكامل للحصول على المساعدة.

الخطوة 1. افهم أن السرعة تُعرّف على أنها معدل التسارع

تعتبر حسابات السرعة عالية المستوى محيرة للغاية لأن علماء الرياضيات والعلماء يستخدمون تعريفات مختلفة لوصف "السرعة" و "التسارع". التسارع مكونان: "معدل" و "اتجاه". المعدل يساوي سرعة الجسم. سيؤدي التغيير في الاتجاه إلى تغيير في التسارع ، ولكن ليس تغييرًا في السرعة.

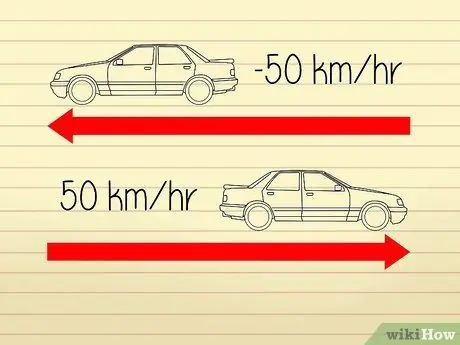
• على سبيل المثال ، لنفترض أن سيارتين تتحركان في اتجاهين متعاكسين. تعرض عدادات السرعة في كلتا السيارتين رقمًا قدره 50 كم / ساعة ، لذا فإن كلاهما يسيران بنفس السرعة. ومع ذلك ، نظرًا لأن السيارات تتحرك بعيدًا عن بعضها البعض ، يمكننا القول أن إحدى السيارتين لديها "تسارع" يبلغ -50 كم / ساعة بينما تبلغ "تسارع" الأخرى 50 كم / ساعة.
• تمامًا مثل حسابات السرعة اللحظية ، يمكنك أيضًا إجراء حسابات تسارع لحظية.

الخطوة 2. استخدم القيم المطلقة لقياس التسارع السالب

يمكن أن يكون للكائن معدل تسارع سلبي (إذا كان يتحرك في اتجاه سلبي بالنسبة لجسم آخر). ومع ذلك ، لا توجد سرعة سلبية. إذن ، في هذه الحالة ، تشير القيمة المطلقة للمعدل إلى سرعة الجسم.

لهذا السبب ، في المثال أعلاه ، تتمتع كلتا السيارتين بسرعة 50 كم / ساعة.

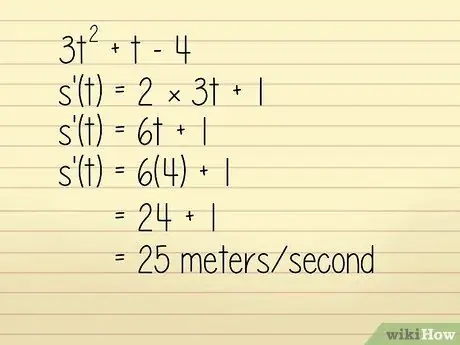
الخطوة 3. خذ مشتق موضع الوظيفة

إذا كانت لديك دالة k (w) تُظهر موضع كائن دون الحاجة إلى حساب الوقت ، فإن مشتق k (w) سيُظهر التسارع دون الحاجة إلى التوقيت. ما عليك سوى إدخال قيمة الوقت في هذه الصيغة بحيث يتم تسريع المتغير w (أو أي قيمة زمنية مستخدمة) وفقًا لذلك الوقت. من هنا ، يمكنك بسهولة إيجاد سرعة الجسم.

• على سبيل المثال ، لنفترض أن موضع الجسم في المتر الواحد موصوف في المعادلة 3q² + w - 4 حيث w = الوقت بالثواني. نريد معرفة سرعة الجسم عند w = 4 ثوانٍ. في هذه الحالة ، يمكنك حلها عن طريق:

  3 واط² + ث - 4

  ك '(ث) = 2 × 3 ث + 1

  ك '(ث) = 6 ث + 1

• الآن ، ندخل w = 4:

  ك '(ث) = 6 (4) + 1 = 24 + 1 = 25 مترا / ثانية. من الناحية الفنية ، هذا هو حساب التسارع ، ولكن نظرًا لأنه موجب والاتجاه غير مذكور في السؤال ، فيمكننا استخدامه لإيجاد السرعة.

الخطوة 4. خذ وظيفة التسريع المتكاملة

التسارع هو طريقة لقياس التغير في تسارع الجسم بمرور الوقت. هذا الموضوع معقد للغاية بحيث لا يمكن شرحه بالكامل في هذه المقالة. ومع ذلك ، من المفيد ملاحظة أنه عندما يكون لديك دالة a (w) تمثل تسارعًا بالنسبة إلى الوقت ، فإن تكامل a (w) سيعيد نتيجة التسارع بناءً على ذلك الوقت. تذكر أنه من المفيد جدًا معرفة التسارع الأولي لجسم ما بحيث يمكنك تحديد ثابت تلك النتيجة من تكامل لا نهائي.

• على سبيل المثال ، لنفترض أن جسمًا ما لديه تسارع ثابت (م / ث² نتيجة ل (ث) = -30. لنفترض أيضًا أن الجسم لديه تسارع ابتدائي قدره 10 م / ث. علينا إيجاد السرعة عند w = 12 ثانية. في هذه الحالة ، يمكننا حلها عن طريق:

  أ (ث) = -30

  p (w) = a (w) dw = -30dw = -30w + C

• لإيجاد C ، سنحل p (w) من أجل w = 0. تذكر أن التسارع الأولي للكائن هو 10 m / s.

  ص (0) = 10 = -30 (0) + ج

  10 = ج ، إذن ف (ث) = -30 ث + 10

• الآن ، يمكننا إدخال w = 12 ثانية.

  ص (12) = -30 (12) + 10 = -360 + 10 = -350. بما أن السرعة هي قيمة مطلقة للتسارع ، فإن سرعة الجسم تساوي 350 متر / ثانية.

نصائح

• الممارسة تجعلها رائعة! حاول إنشاء سؤالك الخاص عن طريق استبدال الأرقام في المثال أعلاه.
• إذا كنت تبحث عن طريقة سريعة لممارسة حساب التفاضل والتكامل من أجل سرعة حساب أفضل ، فاستخدم حاسبة المشتقات عبر الإنترنت هنا والآلة الحاسبة المتكاملة عبر الإنترنت هنا.