- مؤلف Jason Gerald [email protected].
- Public 2024-02-01 14:11.
- آخر تعديل 2025-01-23 12:05.
يشير الإزاحة في الفيزياء إلى تغيير في موضع الجسم. عندما تحسب الإزاحة ، فإنك تحسب المسافة التي يبعدها الجسم بناءً على موقعه المبدئي والنهائي. تعتمد الصيغة التي تستخدمها لحساب الإزاحة على المتغير المعطى للمسألة. اتبع هذه الخطوات لحساب الإزاحة.
خطوة
جزء 1 من 5: حساب النزوح الناتج

الخطوة 1. استخدم معادلة الإزاحة الناتجة إذا تم استخدام وحدة المسافة للإشارة إلى موقعي البداية والنهاية
بالرغم من اختلاف المسافة عن الإزاحة ، فإن مشكلة الإزاحة الناتجة تبحث في عدد الكيلومترات أو الأمتار التي قطعها الجسم. ستستخدم وحدة القياس هذه لحساب الإزاحة ومدى انحراف موقع الكائن عن نقطة البداية.
- تتم كتابة صيغة الإزاحة الناتجة على النحو التالي: S = x² + y². S هو الإزاحة. X هو الاتجاه الأول لحركة الكائن و Y هو الاتجاه الثاني لحركة الجسم. إذا كان الجسم يتحرك في اتجاه واحد فقط ، فإن Y = 0.
- يمكن للكائن أن يتحرك في اتجاهين فقط كحد أقصى لأن التحرك على طول محور شمال / جنوب أو شرق / غرب يعتبر حركة محايدة.

الخطوة 2. قم بتوصيل النقاط بترتيب الحركة وقم بتسميتها من الألف إلى الياء
استخدم مسطرة لرسم خط مستقيم من نقطة إلى أخرى.
- تذكر أيضًا أن تربط نقطة البداية بنقطة النهاية باستخدام خط مستقيم. هذه هي الإزاحة التي سنحسبها.
- على سبيل المثال ، إذا تحرك جسم ما نحو الشرق 300 متر والشمال 400 متر ، فسيشكل مثلث قائم الزاوية. سيكون AB هو الضلع الأول في المثلث ، وسيكون BC هو الضلع الثاني. سيكون AC هو وتر المثلث وحجمه هو إزاحة الجسم. في هذا المثال ، الاتجاهان هما الشرق والشمال.

الخطوة 3. أدخل قيم x² و y²
الآن بعد أن عرفت اتجاهي حركة الكائن الخاص بك ، أدخل القيم في المتغيرات المناسبة.
على سبيل المثال ، x = 300 و y = 400. يجب أن تبدو المعادلة كما يلي: S = 300² + 400²
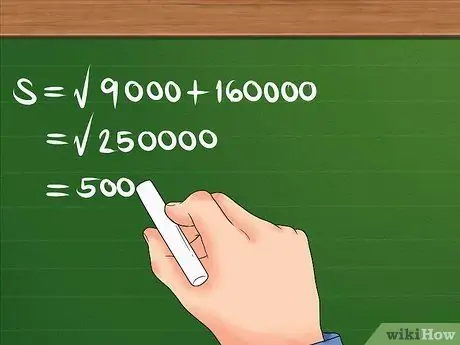
الخطوة 4. احسب المعادلة باستخدام ترتيب العمليات
قم بتربيع 300 و 400 أولًا ، ثم اجمعهما ، وابحث عن الجذر التربيعي للمبلغ.
على سبيل المثال: S = 90000 + 160000. S = 250000. S = 500. الآن تعلم أن الإزاحة 500 م
جزء 2 من 5: عند معرفة السرعة والوقت

الخطوة 1. استخدم هذه الصيغة عندما تخبرك المشكلة بسرعة كائن والوقت الذي يستغرقه
لن تخبرك بعض مسائل الرياضيات بمدى أو مدى سرعة تحرك الجسم. يمكنك حساب الإزاحة باستخدام مقدار الوقت والسرعة.
-
في هذه الحالة ، تصبح الصيغة: S = 1/2 (u + v) ر.
U = السرعة الابتدائية للجسم ، أو مدى السرعة التي يبدأ بها الجسم في التحرك في اتجاه معين. V = السرعة النهائية للجسم ، أو مدى سرعة تحرك الجسم نحو موقعه النهائي. T = الوقت الذي يستغرقه الكائن للوصول إلى موقعه النهائي.
- مثال: تسير السيارة على الطريق لمدة 45 ثانية (الوقت المطلوب). تنعطف السيارة غربًا بسرعة 20 م / ث (السرعة الأولية) وفي نهاية الطريق تكون سرعتها 23 م / ث (السرعة النهائية). احسب الإزاحة بناءً على هذه العوامل.

الخطوة 2. أدخل السرعة والوقت المطلوبين في المتغيرات المناسبة
الآن بعد أن عرفت المسافة التي تتحرك بها السيارة ، ومدى سرعة تحرك السيارة في البداية والنهاية ، يمكنك العثور على المسافة من موقع البداية إلى الموقع النهائي.
يجب أن تبدو معادلتك كما يلي: S = 1/2 (20 + 23) 45

الخطوة 3. احسب الصيغة بعد وضع القيم في المكان الصحيح
تذكر أن تتبع ترتيب العمليات ، وإلا ستؤدي عمليات الإزاحة إلى قيم مختلفة جدًا.
- بالنسبة لهذه الصيغة ، لا يهم إذا قمت بتبديل سرعات البداية والنهاية بطريق الخطأ. نظرًا لأنك ستجمع هذه الأرقام معًا أولاً ، فلا يهم مكان وجودها بين قوسين. ومع ذلك ، بالنسبة للصيغ الأخرى ، سيؤدي تبديل السرعات الأولية والنهائية إلى قيم إزاحة مختلفة.
- يجب أن تبدو معادلتك كما يلي: S = 1/2 (43) 45. قسّم أولًا 43 على 2 ، وهو ما ينتج عنه 21 ، 5. ثم اضرب 21 ، 5 في 45 ، فتكون النتيجة 967.5 مترًا. 967 ، 5 هو مقدار الإزاحة أو المسافة التي قطعتها سيارتك عن نقطة البداية.
جزء 3 من 5: عند معرفة السرعة الأولية والتسارع والوقت
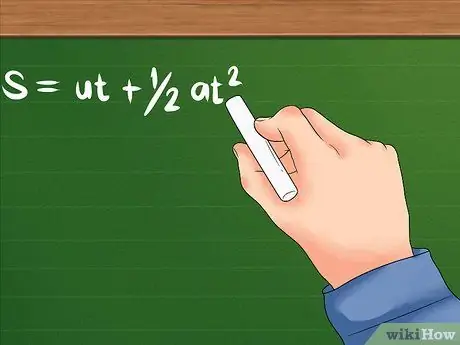
الخطوة 1. استخدم الصيغة المعدلة عندما يكون التسارع معروفًا بالإضافة إلى السرعة والوقت المبدئيين
ستخبرك بعض الأسئلة فقط بمدى سرعة تحرك الجسم في البداية ، ومدى سرعة بدء الجسم في التسارع ، ومدى تحركه. سوف تحتاج إلى الصيغة التالية.
- صيغة هذه المشكلة هي: S = ut + 1 / 2at². لا يزال U يشير إلى السرعة الأولية ؛ أ هو تسارع الجسم ، أو مدى سرعة تغير سرعته. يمكن أن تعني T الوقت الذي يستغرقه أو مقدارًا معينًا من الوقت يستغرقه الجسم للتعجيل. سيستخدم كلاهما وحدات زمنية مثل الثواني والساعات وغيرها.
- لنفترض أن سيارة تتحرك بسرعة 25 م / ث (سرعة ابتدائية) تبدأ في التسارع عند 3 م / ث 2 (تسارع) لمدة 4 ثوان (وقت). ما هي إزاحة السيارة بعد 4 ثوان؟

الخطوة 2. أدخل القيم في الصيغة
على عكس الصيغة السابقة ، يتم تمثيل السرعة الأولية فقط هنا ، لذا تأكد من إدخال البيانات الصحيحة.
بناءً على البيانات النموذجية أعلاه ، ستبدو المعادلة كما يلي: S = 25 (4) + 1/2 (3) 4². من المفيد إضافة أقواس حول مقدار التسارع والوقت لمساعدتك على فصل الأرقام
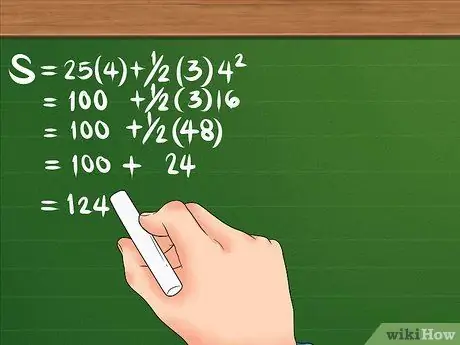
الخطوة 3. احسب الإزاحة عن طريق القيام بذلك بالترتيب الصحيح للعمليات
هناك طريقة سريعة لمساعدتك على تذكر تسلسل العمليات وهي جسر الحمير Kur ir Kua ci Kadang Ba wa Juragan Turtles. يمثل هذا الترتيب الصحيح: الأقواس والمربعات والضرب والقسمة والجمع والطرح.
لنلقِ نظرة على الصيغة مرة أخرى: S = 25 (4) + 1/2 (3) 4². أولًا ، تربيع 4 ، النتيجة هي 16. ثم اضرب 16 في 3 لتحصل على 48 ؛ ثم اضرب 25 في 4 لتحصل على 100. اقسم 48 على 2 لتحصل على 24. يجب أن تبدو معادلتك كما يلي: S = 100 + 24. بمجرد جمع الاثنين معًا ، تكون الإزاحة 124 مترًا
جزء 4 من 5: حساب النزوح الزاوي

الخطوة 1. أوجد الإزاحة الزاوية بينما يتحرك الجسم في مسار دائري
على الرغم من أنك ستظل تحسب الإزاحة باستخدام خط مستقيم ، إلا أنك ستحتاج إلى معرفة الفرق بين موقع بداية ونهاية الكائن أثناء تحركه في مسار دائري.
- تخيل فتاة تجلس على دوامة. عندما يدور مع الكاروسيل ، سوف يتحرك في مسار دائري. تحاول الإزاحة الزاوية إيجاد أقصر مسافة بين الموقعين الابتدائي والنهائي عندما لا يتحرك الجسم في خط مستقيم.
- صيغة الإزاحة الزاوية هي: = S / r ، حيث S هو الإزاحة الخطية ، و r نصف القطر ، والإزاحة الزاوية. الإزاحة الخطية هي المسافة التي يتحرك بها الجسم على طول القوس. نصف القطر هو مسافة الجسم عن مركز الدائرة. الإزاحة الزاوية هي القيمة التي نريد إيجادها.

الخطوة 2. عوّض عن الإزاحة الخطية ونصف القطر في المعادلة
تذكر أن نصف القطر هو المسافة من مركز الدائرة ؛ ستخبرك بعض المسائل بقطر الدائرة التي يجب أن تقسم على 2 لإيجاد نصف القطر.
- إليك مثال لمشكلة: فتاة تركب دوامة. يقع المقعد على بعد متر واحد من مركز الدائرة (نصف القطر). إذا كانت الفتاة تتحرك في مسار قوسي 1.5 متر (إزاحة خطية) ، فما هي إزاحتها الزاوية؟
- ستبدو معادلتك كما يلي: = 1.5 / 1.
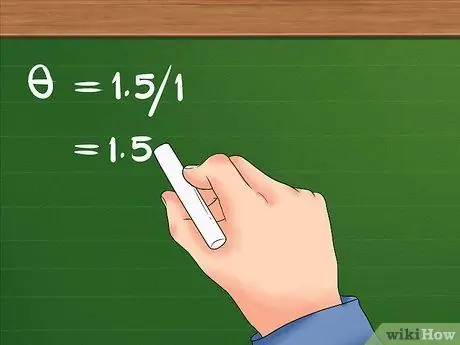
الخطوة 3. قسّم الإزاحة الخطية على نصف القطر
ينتج عن هذا القسمة الإزاحة الزاوية للجسم.
- بعد قسمة 1.5 على 1 ، تكون النتيجة 1.5 ، والإزاحة الزاوية للفتاة هي 1.5 راديان.
- بما أن الإزاحة الزاوية تقيس مقدار دوران الجسم عن موضعه الأولي ، فينبغي قياسه كزاوية وليس كمسافة. الراديان هي الوحدة المستخدمة لقياس الزوايا.
جزء 5 من 5: فهم حول الهجرة
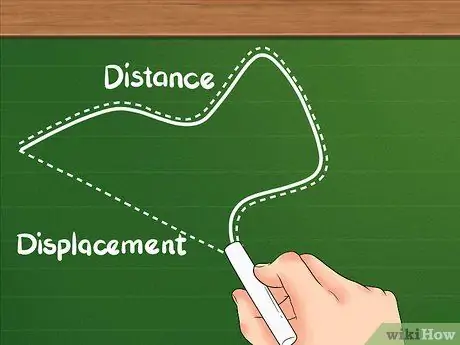
الخطوة 1. تعرف على أن المسافة لها تعريف مختلف عن الإزاحة
تُظهر المسافة المسافة الإجمالية التي يقطعها الجسم.
- غالبًا ما تُعرف المسافة بالكمية العددية. تُظهر المسافة المسافة التي يقطعها جسم ما بغض النظر عن اتجاهه.
- على سبيل المثال ، إذا مشيت خطوتين شرقاً وخطوتين جنوباً وخطوتين غرباً ثم خطوتين شمالاً ، فستعود إلى وضع البداية. على الرغم من أنك قد مررت بالمجموع مسافه: بعد 10 خطوات ، أنت فقط نقل 0 خطوة لأن موقعك النهائي هو نفسه موقع البداية (يشبه المسار الخاص بك مربعًا).

الخطوة 2. افهم أن الإزاحة هي الفرق بين موقعين
النزوح ليس المجموع الكلي للحركة مثل المسافة ؛ تركز التحولات على المنطقة بين مواقع البداية والنهاية.
- يُطلق على الإزاحة كمية متجهة ويظهر التغيير في موضع الكائن من خلال النظر في اتجاه حركة الكائن.
- على سبيل المثال ، أنت تمشي شرقًا لمدة 5 خطوات. إذا عدت إلى الغرب بخمس خطوات ، فستتحرك في الاتجاه المعاكس من موقعك الأصلي. على الرغم من أنك قمت بتغطية 10 خطوات ، فإن وضعك لم يتغير ؛ إزاحتك 0 خطوة.

الخطوة 3. تذكر الكلمات إلى الأمام والخلف عند محاولة تخيل الإزاحة
يؤدي التحرك في الاتجاه المعاكس إلى القضاء على إزاحة الجسم.
تخيل مدرب كرة قدم ذهابًا وإيابًا على الهامش. وبينما كان يصرخ على اللاعبين ، انتقل من اليسار إلى اليمين عدة مرات. إذا شاهدته وهو يتحرك من اليسار إلى اليمين ، فإنك تلاحظ المسافة الإجمالية التي قطعها. ومع ذلك ، افترض أن المدرب توقف للتحدث إلى لاعب الوسط على الهامش. إذا كان في نقطة مختلفة عن مكانه الأصلي قبل الانتقال ، فأنت تراقب حركة المدرب

الخطوة 4. اعلم أن الإزاحة تُقاس باستخدام مسار مستقيم ، وليس مسارًا دائريًا
لإيجاد الإزاحة ، عليك أن تجد الطريقة الأقصر والأكثر فاعلية لحساب الفرق بين نقطتين.
- سيأخذك المسار الدائري من موقع البداية إلى موقعك النهائي ، لكنه ليس أقصر طريق. لمساعدتك على تصور ذلك ، تخيل أنك تمشي في خط مستقيم وصادفت عمودًا. لا يمكنك اختراق هذا العمود ، لذا عليك الالتفاف حوله. على الرغم من أن موقعك النهائي هو نفسه كما لو كنت قد اخترقت العمود ، فستحتاج إلى خطوات إضافية للوصول إلى هذا الهدف.
- على الرغم من أن الإزاحة تمثل مسارًا مستقيمًا ، فاعلم أنه يمكنك قياس إزاحة الجسم حاليا تتحرك في مسار دائري. يسمى هذا الإزاحة بالإزاحة الزاوية ويمكن حسابها بإيجاد أقصر مسار من الموقع الأولي إلى الموقع النهائي.

الخطوة 5. اعرف أن الإزاحة يمكن أن تكون سالبة ، على عكس المسافة
إذا تم الوصول إلى موقعك النهائي بالتحرك في الاتجاه المعاكس لاتجاهك الأولي ، فإن إزاحتك تكون سالبة.
- على سبيل المثال ، نسير 5 خطوات شرقا ثم 3 خطوات غربا. على الرغم من أنك تتحرك بخطوتين من موقع البداية عن طريق الحساب ، فإن إزاحتك هي -2 لأنك تتحرك في الاتجاه المعاكس. ستكون المسافة دائمًا موجبة لأنه لا يمكنك العد التنازلي بالخطوات والكيلومترات وما إلى ذلك.
- الإزاحة السالبة لا تعني أن الإزاحة تقل. السلبي يعني فقط أن الاتجاه معاكس.

الخطوة 6. ندرك أنه في بعض الأحيان يمكن أن تكون المسافة والإزاحة نفس الشيء
إذا مشيت بخط مستقيم 25 خطوة وتوقفت ، فستكون المسافة التي تقطعها مساوية للإزاحة من موقعك الأصلي.
- ينطبق هذا فقط عندما تنتقل من موقع واحد من موقع البداية في خط مستقيم. على سبيل المثال ، أنت تعيش في سان فرانسيسكو ، كاليفورنيا ، وتحصل على وظيفة جديدة في لاس فيجاس ، نيفادا. عليك أن تنتقل إلى لاس فيغاس لتكون قريبًا من وظيفتك. إذا ركبت طائرة تطير مباشرة من سان فرانسيسكو إلى لاس فيجاس ، ستقطع المسافة نفسها والإزاحة x.
- ومع ذلك ، إذا كنت تقود سيارتك من سان فرانسيسكو إلى لاس فيجاس ، فستقطع مسافة x ، لكنك ستقطع مسافة y. نظرًا لأن قيادة السيارة لها اتجاهات متغيرة عادةً (شرق هذا الطريق ، غرب ذلك الطريق) ، فسوف تسافر لمسافات أطول من أقصر مسافة بين المدينتين.






